摘(zhai)要:本文(wén)提供了(le)使用差(cha)壓流量(liang)計 測量(liàng)氣體流(liu)量時壓(yā)縮系數(shù)的建模(mo)方法。該(gāi)文闡述(shù)⭐了通過(guo)㊙️建🈲立數(shu)學模型(xíng),并通過(guo)數學模(mó)型得到(dào)了壓🌍縮(suo)系數的(de)運算公(gōng)式🤩,與試(shi)驗結果(guo)一緻。通(tong)過對計(jì)算🔞公式(shi)的分析(xi),得到了(le)管道和(hé)孔闆的(de)幾💋何參(can)數對壓(ya)縮系數(shù)的.影響(xiǎng)。
1概述
　　流(liu)量計曆(lì)史悠久(jiu),在各行(hang)各業中(zhong)廣泛應(ying)用,研究(jiu)人員一(yī)❓直進行(hang)着對其(qi)的改進(jìn)研究.2。差(chà)壓流量(liàng)計的準(zhun)确性取(qu)決于流(liu)💜量系數(shu)的值,實(shi)際流量(liàng)與理論(lùn)流量的(de)比值稱(cheng)爲流量(liang)系數。流(liú)量系數(shù)收到很(hen)多因素(sù)的影響(xiǎng)，這些因(yin)素構成(cheng)了差壓(yā)法測量(liang)的基💯礎(chǔ)。其中一(yī)個因素(sù)是壓❤️縮(suō)系數,其(qí)在通過(guo)測量孔(kong)59671之後産(chǎn)生。流量(liang)計測量(liang)的誤差(chà)受到額(é)外收縮(suo)的影響(xiang)。差壓流(liu)量🐅計相(xiang)關文獻(xian)中直接(jiē)研究額(e)外收縮(suō)♌的很少(shao)。
　　在推導(dao)差壓流(liú)量計計(ji)算公式(shì)時,收縮(suo)系數作(zuo)爲孔徑(jìng)系🏒數的(de)部分進(jin)行考慮(lü)。Alvi在工作(zuò)四中嘗(cháng)試确定(dìng)收縮系(xì)數,後🐅來(lái)Kremlevsky5I對收縮(suō)系數進(jin)行了理(li)論建模(mo)。該系數(shu)與流量(liang)計的設(she)計和取(qu)壓方式(shi)有關。文(wén)獻[9,10]詳細(xì)介紹了(le)取壓方(fāng)式對收(shōu)縮系數(shu)的影響(xiang)。節流件(jian)厚度影(ying)響🐉在文(wén)獻[11,12]中進(jin)行了介(jie)紹。描述(shù)了收縮(suo)過程及(jí)其在管(guan)🔅道系統(tong)中産生(sheng)👣的影響(xiang)。
　　收縮系(xì)數在測(ce)量流量(liang)時也會(hui)影響氣(qì)體流量(liàng)膨脹系(xi)數。對❄️于(yu)噴嘴和(hé)文丘裏(li)管,其值(zhí)取爲--緻(zhì),當使用(yòng)孔闆測(cè)量氣體(tǐ)流量時(shi),收縮系(xì)數成爲(wèi)膨脹系(xì)數經驗(yàn)公式的(de)🔴--部分裏(lǐ)。從這些(xiē)研究中(zhōng)💞可以清(qīng)楚地看(kan)出,該系(xi)數與管(guan)道和孔(kǒng)闆的幾(jǐ)何參數(shu)密切相(xiang)🏃關,因此(ci)它成爲(wei)差壓流(liú)量計模(mó)型中使(shi)用的系(xi)數的-部(bù)分。爲了(le)評估其(qi)對流量(liang)測量過(guo)程的影(yǐng)響,本文(wen)提出了(le)更準确(que)的方法(fa)。
在本文(wén)中,我們(men)考慮該(gāi)過程的(de)建模和(he)收縮系(xi)數的計(ji)算,充分(fen)估計收(shōu)縮值并(bing)預測其(qí)在測量(liàng)期間的(de)行爲。
2建(jian)模
　　爲了(le)解決這(zhe)個問題(tí),作者在(zai)測量儀(yí)表運行(háng)時使用(yong)💋了流量(liàng)分布✔️的(de)數學描(miao)述。圖1展(zhan)示差壓(ya)法測流(liú)量的剖(pōu)面圖。該(gāi)圖顯示(shi)了✨液體(ti)😘或氣體(ti)流量的(de)穩态曲(qǔ)線,這将(jiang)作爲解(jiě)決💔問題(ti)的基礎(chǔ)。本文是(shi)利用幾(ji)何流量(liàng)剖面來(lai)尋找與(yu)流量測(cè)量方法(fa)有關的(de)物理量(liang)。在流📱量(liàng)計行程(cheng)内，流量(liàng)分布可(ke)以通過(guò)X0Y平面🎯中(zhōng)的函數(shu)來描述(shù),結果,可(kě)㊙️以🏃🏻獲得(de)流量計(jì)裝置的(de)所有必(bì)要特性(xing)。在測量(liang)管🔞道中(zhong)帶有 孔(kǒng)闆流量(liang)計 ,其中(zhōng)靜止的(de)氣體或(huo)流體可(kě)以表示(shì)爲以下(xia)等式:

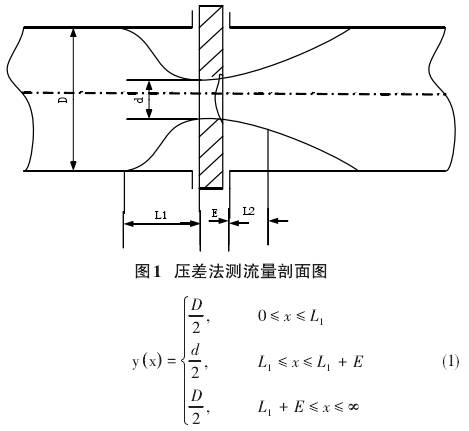
　　其(qí)中D--測量(liàng)管道的(de)直徑,d-孔(kǒng)闆孔的(de)直徑,L1--流(liu)動未受(shou)幹擾的(de)孔闆前(qian)壓力分(fen)流的距(ju)離,E-孔闆(pan)厚度,x-方(fang)向坐标(biao)。圖2中的(de)曲線圖(tú)完全描(miao)述了儀(yí)表運行(háng)中靜止(zhǐ)流量的(de)曲線,對(duì)應于該(gāi)等式。該(gai)技術涉(she)及在XOY平(ping)面中找(zhao)到⭕功能(neng)，其完全(quan)描述了(le)流量計(ji)系統的(de)流量🏃🏻‍♂️計(jì)運行時(shí)㊙️的幾何(hé)流動剖(pou)面。

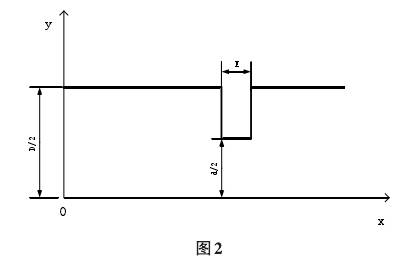
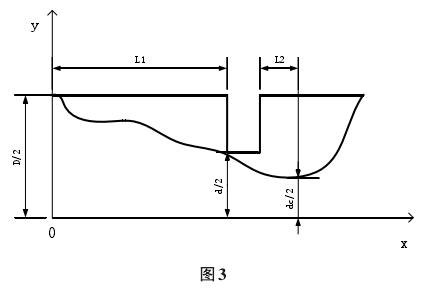
　　本文(wén)目的是(shì)找到一(yī)個變量(liàng)的函數(shù),該變量(liàng)最接近(jin)地描述(shù)🍉通過流(liú)量傳感(gǎn)器的幾(ji)何流動(dong)剖面。在(zài)所考❌慮(lǜ)的領域(yu),這種功(gōng)能應該(gai)是平穩(wen)和可區(qu)分的。另(ling)一方面(mian)，它應該(gāi)簡單易(yi)用。因此(ci),使用指(zhǐ)數函數(shù)描述流(liú)動剖面(mian)模型。該(gāi)功能應(ying)取決于(yu)管道的(de)幾何參(can)數,孔㊙️闆(pǎn)和影響(xiǎng)幾🌈何流(liú)動剖面(miàn)的距離(lí)。通過孔(kong)闆形成(chéng)的幾何(hé)流動剖(pou)面🌏的影(ying)響參數(shu)的研究(jiu)使得作(zuò)者📧以等(děng)式(2)的形(xíng)式得到(dào)了🧡流動(dong)剖面的(de)數學模(mo)型。
因此(ci),可以通(tong)過以下(xia)等式描(miáo)述具有(you)圖3中表(biao)示的移(yí)動🛀🏻流量(liàng)的流量(liàng)計:

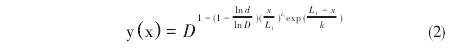
　　其中(zhōng)D-測量管(guǎn)道的直(zhí)徑,d-孔闆(pan)孔的直(zhi)徑,L1一流(liú)動未受(shou)幹🌐擾的(de)孔闆♌前(qian)壓力分(fèn)流的距(ju)離,L2-VenaContracta孔闆(pǎn)後壓.力(lì)分流的(de)距離，x-方(fāng)☀️向坐标(biao),k-與附加(jia)收縮位(wèi)置相關(guan)的一-些(xiē)系數。從(cong)圖1中可(kě)以看出(chu),孔闆由(you)孔d的直(zhí)徑和孔(kǒng)闆E的厚(hòu)度确定(ding)。孔闆的(de)厚度與(yǔ)長度L1[4]有(you)關。
　　公式(shì)(2)給出的(de)函數完(wán)全描述(shù)了圖3中(zhōng)所示的(de)儀表運(yun)行中的(de)幾何流(liu)動剖面(mian)。假設流(liú)動關于(yu)0X軸對稱(cheng)。該圖還(hái)顯示,在(zài).VenaContracta處,該儀(yí)表🤞行程(cheng)的直徑(jing)de小于孔(kǒng)闆孔的(de)直徑d。因(yīn)此,我們(men)的目标(biao)是🚶‍♀️獲得(de)直徑de的(de)精确表(biǎo)達式。我(wǒ)👄們的方(fang)法基于(yu)使用基(jī)于流動(dong)🎯剖面的(de)幾何依(yi)賴性的(de)方程來(lái)描述它(tā)們的流(liu)體動力(lì)學特🐆征(zheng)。

　　爲了求(qiu)收縮腔(qiang)的直徑(jìng),需要從(cong)收縮腔(qiang)的坐标(biāo)中求出(chu)💯函✂️數(2)的(de)值💔。如果(guo)我們知(zhī)道函數(shu)(2)在原點(dian)處具有(you)測量管(guǎn)道直徑(jing)y(0)=d/2的值,那(nà)麽在距(jù)離l1處具(jù)有孔闆(pǎn)孔直徑(jìng)y(1)=d/2的值,如(ru)圖.3和圖(tú)4所示。

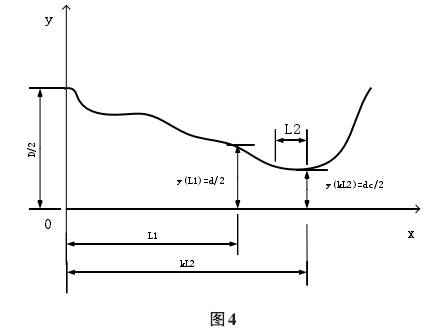
　　縮(suo)窄靜脈(mò)與孔闆(pǎn)12後的距(ju)離有關(guān),在流量(liàng)測量組(zǔ)織中起(qǐ)着重要(yao)作用。假(jia)設收縮(suō)靜脈的(de)坐标與(yu)某個系(xì)數k有關(guan),該系數(shù)決定了(le)收縮靜(jing)脈的直(zhí)徑y(kl2)=dc/2。
3收縮(suo)系數建(jian)模
根據(jù)文獻[5,7],收(shōu)縮系數(shù)定義爲(wèi)縮窄靜(jìng)脈面積(jī)與孔闆(pǎn)孔面積(jī)之比:

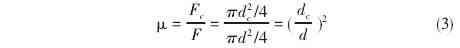
式(shi)中:Fc-一靜(jìng)脈收縮(suō)面積,F一(yi)孔闆孔(kong)面積。
　　我(wo)們知道(dào)所需的(de)系數取(qu)決于流(liu)量的幾(jǐ)何結構(gòu),在孔的(de)相對直(zhi)徑上闆(pǎn)β=dD以及孔(kǒng)闆L和L，前(qian)後的距(jù)離。讓我(wǒ)們将距(ju)離L2與系(xi)數k聯系(xi)起來,這(zhe)将起到(dào)主要作(zuò)用。系數(shu)k取決于(yu)收縮系(xì)數,以及(jí)其他相(xiang)關參數(shu)。
我們将(jiang)方程(2)改(gǎi)寫爲:它(tā)僅取決(jue)于我們(men)的流量(liàng)幾何參(cān)🈚數🌈k、L1L2和🐅β:

　　可(kě)以看出(chū)，最後一(yi)個方程(cheng)取決于(yu)流量幾(ji)何參數(shu),但系數(shù)k的值仍(réng)然未知(zhī)。因此，對(dui)于圖3所(suo)示的剩(sheng)餘參數(shù)和條件(jian)的已知(zhi)值,搜索(suo)系數k的(de)另一個(ge)問題将(jiāng)提供收(shōu)縮系數(shu)的适當(dāng)計算。以(yǐ)這種方(fang)式提出(chu)的問題(tí)導緻我(wǒ)們得出(chu)以下μ值(zhi)所需系(xì)數的表(biǎo)達式:

　　因(yin)此,我們(men)得到了(le)一個簡(jian)單的方(fang)程,通過(guò)以簡單(dan)函📞數🌍的(de)形式模(mo)拟流量(liàng)計運行(hang)中的流(liu)量分布(bu),計算收(shōu)㊙️縮系數(shù)。從🐆方程(chéng)(7)可以看(kan)出,收縮(suo)系數完(wán)全取決(jué)于相對(duì)直徑✌️β。
　　提(tí)出的研(yan)究允許(xǔ)模拟收(shōu)縮系數(shù)的值,這(zhe)是基于(yú)描述的(de)幾何㊙️形(xing)式的流(liu)量剖面(miàn)。指定該(gai)系數有(you)助于研(yán)究和完(wán)善🏃‍♂️流量(liàng)系數。
4結(jie)果和讨(tao)論
　　我們(men)将使用(yòng)公式(7)對(duì)收縮系(xì)數的表(biao)達式進(jin)行研究(jiū)🛀,并将其(qi)☀️與早期(qī)的實驗(yan)工作進(jìn)行比較(jiào)。圖5顯示(shi)了收縮(suo)系數的(de)圖形。
　　在(zai)圖5中,圖(tu)1根據公(gōng)式(7)提供(gong)相關性(xing),圖2表示(shi)實驗alvi曲(qǔ)線[5,7],圖❗3表(biǎo)示Kremlevsky[5]建立(li)的相關(guān)性，圖4表(biao)示來自(zì)bumer.工作的(de)曲線[15]。
　　圖(tú)6顯示了(le)收縮系(xì)數與孔(kong)闆相對(duì)直徑的(de)關系。這(zhè)種依💘賴(lai)性⛱️完全(quán)由公式(shi)(7)構成。結(jié)果表明(ming),所有與(yu)收縮有(you)關的現(xiàn)象都被(bèi)🔞簡化爲(wèi)收縮系(xì)數與相(xiàng)對直徑(jìng)的依賴(lai)關系。公(gong)式(7)的推(tui)導證明(ming)了這一(yi)點。确定(ding)收縮過(guò)程的所(suo)有流⁉️量(liang)參數都(dou)隻與相(xiang)對直徑(jìng)有關,這(zhe)與[4,5,7]中的(de)實驗研(yán)究很吻(wěn)合。

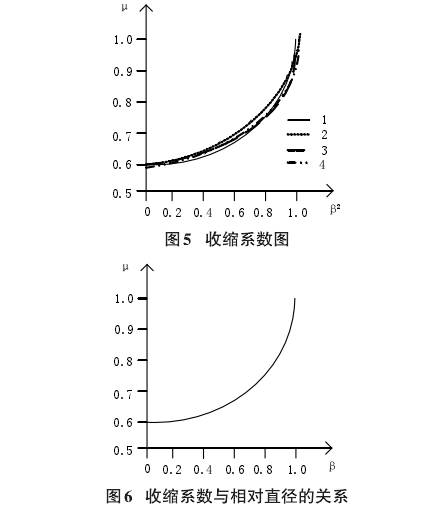
　　從圖(tu)5中的圖(tú)表可以(yi)看出,2和(hé)3的依賴(lài)關系更(geng)爲接近(jin)✂️。這💘兩條(tiao)㊙️曲✉️線都(dou)是在不(bu)同的時(shi)間得到(dao)的,與實(shí)驗結果(guo)吻合較(jiào)好。曲🥰線(xiàn)1是通過(guo)分析得(dé)出的，與(yu)早期的(de)研究結(jie)果(與曲(qǔ)線2和3相(xiàng)比)并不(bú)矛盾。圖(tu)7給出了(le)獲得的(de)方程(7)相(xiàng)對于實(shí)驗阿爾(er)維曲線(xian)的相對(dui)誤⛷️差估(gū)計:

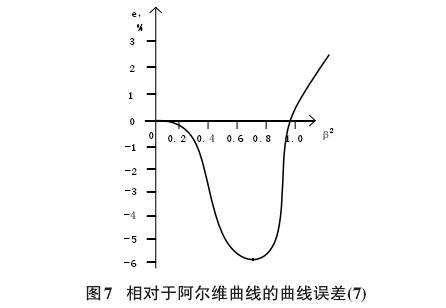
　　從圖(tu)7的方案(àn)可以看(kan)出,現有(yǒu)結果與(yǔ)方程(7)之(zhi)間的最(zui)👣大差💯異(yì)是💋随着(zhe)相對孔(kong)闆的增(zeng)加而實(shi)現的。方(fāng)程式(7)數(shu)據與ALVI結(jie)㊙️果之☁️間(jiān)的最小(xiao)誤差在(zai)β<0.4時得到(dào)。
　　這項工(gōng)作的另(lìng)-一個結(jié)果是,利(li)用導出(chu)方程式(shi)(7)的公式(shi)計🧑🏾‍🤝‍🧑🏼算收(shou)縮坐标(biāo)和所需(xu)的取壓(yā)口長度(du)的可能(neng)性👄。知道(dào)系數k的(de)值,就可(ke)以得到(dao)流/流區(qu)的任何(he)橫截面(miàn)的值;因(yin)此,确定(ding)距離所(suo)需橫截(jié)面采用(yòng)公式(6)。圖(tu)8顯示了(le)允許我(wǒ)🔞們根據(ju)孔闆的(de)相對直(zhi)徑确定(dìng)該系數(shù)值之間(jian)關系的(de)圖。在這(zhè)種情況(kuang)下,觀察(chá)到,随着(zhe)孔闆.前(qián)流量計(jì)運行長(zhǎng)度的增(zēng)加,系數(shu)的值減(jiǎn)小。圖8中(zhong)的依賴(lai)關系是(shì)在系數(shu)k的某些(xie)值下得(de)到的,必(bì)須确定(dìng)這些值(zhí)。

　　如上圖(tú)所示,本(ben)文展示(shi)了描述(shu)流量剖(pōu)面的方(fāng)程與使(shi)用這🥵些(xie)剖面确(què)定的值(zhí)之間的(de)關系。該(gai)方法的(de)有效性(xing)體現在(zai)求解問(wèn)題中,得(dé)到了流(liu)動收縮(suo)系數的(de)🏃🏻‍♂️解析表(biao)達式,與(yǔ)實驗結(jié)⚽果吻合(he)較好。這(zhe)項技術(shu)的另☎️--個(gè)結果是(shì)開發了(le)計算用(yong)于确定(dìng)穩定或(huo)壓力分(fèn)接頭的(de)儀表運(yùn)行系數(shù)的方🌏法(fǎ)。從圖6可(ke)以看出(chū),孔闆前(qián)後的長(zhǎng)度取決(jué)于相對(duì)直徑,并(bing)通過系(xi)數k相互(hù)關聯👈。
5結(jie)論與未(wei)來工作(zuò)
　　本文提(ti)出了一(yi)個新的(de)收縮系(xì)數計算(suan)公式。文(wen)中給出(chu)了從描(miao)述🧡幾何(he)流剖面(miàn)的方程(cheng)中獲得(de)收縮系(xi)數的可(kě)能性。研(yan)究結果(guǒ)表明,流(liu)量收縮(suō)系數與(yu)孔闆相(xiàng)☎️對直徑(jing)之間存(cún)在一-定(dìng)的關系(xi)❓,可以通(tong)過特殊(shu)的蘭🌂伯(bo)特函數(shù)⁉️求得孔(kong)闆相對(duì)直徑。得(dé)到了收(shou)縮系數(shu)與👨‍❤️‍👨相對(dui)直徑及(ji)其平方(fāng)的關🔆系(xi),與實驗(yàn)結果吻(wen)合較好(hǎo)😍。這種方(fāng)法的🙇‍♀️結(jié)果是能(néng)夠計算(suàn)出流體(ti)和氣體(ti)流量測(ce)量過程(cheng)中的取(qu)壓口距(jù)離。這種(zhong)方法還(hái)可以獲(huo)得與✔️流(liu)動的幾(jǐ)何輪廓(kuò)和管道(dao)中流動(dòng)物質直(zhí)接相關(guan)的其他(tā)流動參(can)數。本研(yán)🈚究的作(zuo)者将繼(jì)續發展(zhan)這種✌️方(fang)法,以改(gai)進流量(liàng)計系統(tǒng)的模型(xing)。

以上内(nei)容源于(yú)網絡，如(ru)有侵權(quán)聯系即(ji)删除!