1 引言
    近年以來，随(suí)着流量計量行業(yè)的發展， 電磁流量(liàng)計 以其無可動部(bu)件、無壓力損失、測(cè)量量程範圍寬等(deng)優點應用于各種(zhǒng)場合，而在使用過(guò)程中遇到的一個(ge)難⭐題就是如何提(ti)高大口徑大流量(liang)計量的準确✨度。如(ru)果✉️使用 管道式電(dian)磁流量計 測量大(da)口徑管道流量，則(ze)其體積大、加工成(chéng)本高并且标定和(hé)安❤️裝維修都十分(fen)困難，給工程應用(yòng)帶來很多不便。所(suǒ)以在這種情㊙️況下(xia)，一般用插入式電(dian)磁流量計 代替管(guan)道式電磁流量計(jì)用于測量大口徑(jìng)管道的流量。
    但是(shi)插入式電磁流量(liàng)計會産生非線性(xing)現象，影響💁測量的(de)準确性。現在很多(duo)學者解決這個問(wèn)題多采用的是多(duō)🔴段非線性補償方(fang)法，把整個量程範(fàn)圍裏✏️面的流量分(fen)成多個流量段, 再(zai)分别求☔解出不同(tong)階段的流量系數(shù)，從而可以得出⛷️各(gè)段的流量值。但是(shì)這種方法使用起(qi)來比較複雜，且精(jing)度也受到了限制(zhì)。所以本文⭐從電磁(ci)流量計自身結構(gòu)出發，找出産生非(fei)線性現象的原因(yīn)，從源頭上找出提(tí)高插入式🈲電磁流(liú)量計線性度的方(fang)法。
2 插入式電磁流(liú)量計工作原理
    插(chā)入式電磁流量計(ji)測量原理［1］是基于(yú)法拉第電磁感🐆應(yīng)定律

    其中，E 爲兩電(diàn)極之間産生的感(gǎn)應電動勢，B 爲磁感(gan)應強度👌，L爲切割磁(ci)感線的有效長度(du)，v珋 爲平均流速，流(liu)質爲🥵導電介質，原(yuán)理圖如圖 1 所示。
并(bing)且( 1) 式經變換可表(biao)示爲

當 B 和 L 都爲常(cháng)數時，隻要測得感(gǎn)應電動勢 E 就可以(yi)得到平均流速ν? ，因(yin)被測管道的橫截(jie)面積已知，這樣就(jiù)可以很容易求得(dé)某導電流質的體(tǐ)積流量

    其中，D 爲被(bèi)測管道内徑，Qv爲體(tǐ)積流量。由( 3) 式可知(zhī)，當插入管💯道結構(gòu)一定時，體積流量(liàng) Qv與比值 E/B 成正比，而(ér)與流體的溫🐕度、密(mi)度、管内壓力等無(wu)關。當磁感應強度(dù)B爲常數時，體積流(liú)量Qv與感應電動勢(shì)E成正比，即體積流(liú)量與感應電動勢(shi)之間是完全呈線(xiàn)性🔞關系的。
    由( 3) 式可(ke)知，當插入管道結(jie)構一定時，體積流(liú)量 Qv與比⭐值 E/B 成正比(bǐ)，而與流體的溫度(dù)、密度、管内壓力等(deng)無關。當磁感應強(qiáng)度B爲常數時，體積(ji)流量Qv與感應電動(dòng)勢E成正比，即體積(jī)流量與㊙️感應電動(dòng)勢之間是完全呈(cheng)線性關系的。
3 傳感(gǎn)器線性度評定
    線(xiàn)性度［2］是傳感器的(de)主要靜态性能指(zhi)标之一，其定義爲(wèi)測試系統的輸出(chū)和輸入系統能否(fou)像理想系統那樣(yang)保持正常值比例(li)關系( 線性關系) 的(de)一種度量。線性度(dù)反應了校準曲線(xiàn)與某一規🌂定直線(xian)一緻的程度，此🔞規(gui)定直線即爲按一(yī)定方法确定的理(li)想直線。線性度又(you)稱爲非線性度，參(can)考GB/T18459 －2001《傳感器主要靜(jìng)态性能指标計算(suàn)方法》中的線性度(du)定義: 正、反行程實(shí)際平均特性曲線(xian)相對于參比直線(xian)( 拟合直線) 的最大(dà)偏差，用滿量程🔞輸(shu)出的百分比來表(biǎo)示。這一指💜标通常(chang)以線性誤差表示(shi)

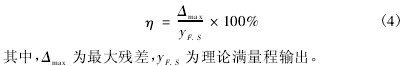
    本文采用最小二(er)乘法進行線性度(dù)評定，即拟合直線(xian)爲❄️最💛小二乘直線(xiàn)。最小二乘直線保(bao)證了傳感器實際(jì)輸出的平均值對(dui)它 的偏差的平方(fāng)和爲最小，即可以(yǐ)保證拟合直線得(de)到的結果與實測(ce)結果之間的偏差(chà)很小，更具可靠性(xing)。根據定義，線性度(dù)即是校準曲線對(dui)🚶‍♀️這條最小二乘拟(ni)合直線的偏離程(chéng)度。
4 插入式電磁流(liu)量計非線性現象(xiàng)成因
    插入式電磁(ci)流量計使用時在(zai)被測管道合适位(wèi)置處❤️打孔插入以(yǐ)測量導電流體流(liú)量，并且可以在不(bú)斷流的情況下取(qu)出進行清洗和維(wei)修，操作十分方便(bian)。但是插入管道的(de)探頭對于管道流(liu)場來說，相當于引(yin)入了一個阻流器(qi)件，流體🔞對此探頭(tóu)進行繞流運動，如(rú)圖 2 所示。

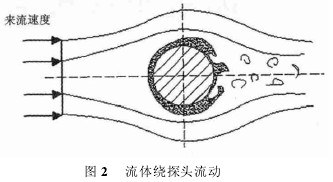
    流(liu)體繞探頭流動時(shi)，由于粘性力的存(cun)在，在探頭表面👄會(huì)形💋成邊界層。随着(zhe)流體沿曲面上下(xià)繞流，邊界層厚度(dù)越來越大。越靠近(jin)壁面的地方，其流(liú)場的變化越複雜(zá)［3］。而流場分布的變(biàn)化會擴大被測平(ping)均流💋速與實際來(lai)流速度之間的誤(wù)差。并且在逆壓強(qiang)梯度足夠大的時(shi)候會産生回流導(dǎo)緻邊界層分離，并(bìng)🔞形成尾渦，即産🐪生(sheng)邊界層分離現象(xiang)，這會使非線性現(xiàn)象加劇。即是被測(cè)平均流速與來🈲流(liu)速度之間的🤩非線(xiàn)性導緻了感應電(dian)動勢與被測流🤩量(liang)之間線性關系遭(zao)到破壞，使插入式(shi)電磁流量計測量(liàng)的準确🐆度降低。
    影(ying)響這一線性關系(xi)的因素有許多，主(zhu)要有插入式電磁(cí)💰流⛱️量計的安裝角(jiao)度［4］、插入深度、探頭(tóu)形狀等等。其中安(ān)裝角度和插入深(shen)🏃‍♂️度對輸入輸出信(xìn)号間線性關系的(de)影響可以通過正(zhèng)确☂️安裝流💚量計和(hé)标定實驗來得以(yǐ)消除。所以本文所(suo)研究的影響插入(ru)式電磁流 量計線(xian)性度的原因主要(yao)是插🔆入管道内的(de)🙇‍♀️探頭形狀，不同🌈探(tàn)頭形狀對管🏃🏻内流(liú)場分布狀況的💚影(ying)響不盡相同。
    本文(wén)通過 FLUENT 軟件對四種(zhong)不同形狀的插入(ru)探頭對管道流☀️場(chǎng)的🔞影響進行了三(san)維仿真，在 0． 5m/s ～ 15m/s 範圍内(nei)，選取其中典型的(de)幾個速度點作爲(wèi)入口速度，以垂直(zhí)于來流方向兩電(diàn)極所在截面的平(ping)🐆均流速作爲信号(hào)采集到的平均流(liú)速，通過拟合得到(dào)它們之間的關系(xi)。根據比較不💯同形(xíng)狀探頭情況下得(dé)到的最小二乘拟(ni)合直線所求出的(de)流速與實際流速(su)之間偏差的🌈大小(xiǎo)來評判線性度的(de)優劣，從而可💋以得(de)到線性度的一種(zhong)探頭類型。
5 數值模(mo)型設計
    本文利用(yong)前處理軟件 GAMBIT 構建(jian)工程上四種常見(jian)的插入式🔴電磁流(liú)🌈量計探頭形狀，如(ru)圖 3 所示。設定管道(dao)内徑爲⚽400mm，插入深度(dù)✔️爲 120mm，探頭半徑爲 32mm，電(dian)極半徑爲5mm。
5．1 湍流模(mó)型
    本文的湍流模(mó)型采用工程上使(shǐ)用廣泛的标準k－ε模(mó)型，需要求解湍動(dong)能及其耗散率方(fang)程。在該模型中，有(yǒu)關湍動能k和耗散(san)🐕率ε的運輸方程如(rú)下


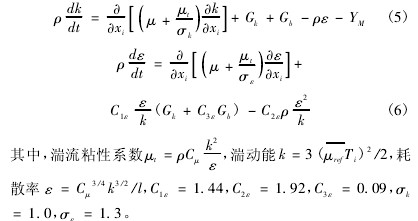
5．2 網格劃分
    用 GAMBIT 軟(ruan)件對流場進行網(wǎng)格劃分，因要模拟(nǐ)的是三維流場計(ji)算區域，在既要保(bao)證精度的前提下(xia)又要盡可能使運(yun)算簡☂️便，故❗在靠近(jin)探頭周圍區域劃(huà)分出密一點的網(wang)格，而在前後直管(guan)☁️段區域劃分出相(xiàng)對稀一點的網格(ge)，以滿足計算要求(qiú)。本文使用的網格(gé)🤞格式單元是 Tet/Hybrid，指定(ding)的格式類型是 TGrid，表(biǎo)明指定網格主🐆要(yào)由四面體網格構(gòu)成，但是在适當的(de)位置可以包含六(liu)面體、錐形和楔形(xing)網格單元。
5．3 建立離(li)散化方程
    本文使(shi)用現今工程上應(ying)用廣泛的有限體(tǐ)積法［6］，将計算🏃區域(yù)劃⛹🏻‍♀️分爲一系列控(kong)制體積，并在每一(yi)個控制體😘積上對(dui)待解微分方程積(ji)分，得出離散方程(chéng)。在這些控制體上(shàng)求解質量、動量、能(néng)量、組🔴分等的通用(yong)守恒方程

    其中，左(zuǒ)邊第一項爲瞬态(tài)項，第二項爲對流(liu)項，右邊第一㊙️項爲(wèi)擴散項，第二項爲(wèi)通用源項。方程中(zhōng)的 φ 是廣義變量，可(kě)以表示😘一些待求(qiu)的物理量如速度(dù)、溫度、壓力等，Γ 是相(xiàng)應于 φ 的🙇‍♀️廣義擴散(san)系數，變量 φ 在端點(diǎn)😄的邊界值爲已知(zhī)。
在控制方程中使(shi)用了 SIMPLE 算法，是屬于(yu)壓力修正法的一(yī)種🍓; 并且👣采用了二(er)階迎風格式，使計(jì)算結果更加🌍準确(què)❓。
5． 4 确定邊界條件
    實(shi)驗以常溫常壓下(xià)水( 20℃、1atm) 爲流入管道的(de)流質，設定管道入(ru)口邊界條件爲速(sù)度入口，管道出口(kǒu)邊界條件㊙️爲壓🧑🏾‍🤝‍🧑🏼力(lì)出♈口。選取以下 8 個(ge)速度點進行仿真(zhēn): 0． 5m/s、1． 0m/s、2．5m / s、5m / s、7． 5m / s、10m / s、12． 5m / s、15m / s，觀察其流場分布(bù)，可以得到信😄号采(cai)集⁉️到的平均流速(su)。
6 仿真結果與計算(suàn)比對
    通過 FLUENT 仿真，可(ke)以看到由于探頭(tóu)的插入，流質對探(tàn)頭進🐅行繞流運動(dòng)，導緻管道内流場(chang)發生了變化，破壞(huai)☎️了流場穩定性☔，即(ji)是這種變化導緻(zhi)了插入式電磁流(liu)量計輸入輸🔴出信(xin)号之間的線性度(dù)降低。同時還可以(yǐ)得到在0． 5m/s ～ 15m/s的流速範(fan)圍内，不同來流速(su)度下信号采集到(dào)的平💚均流速，得到(dào)如下表 1。

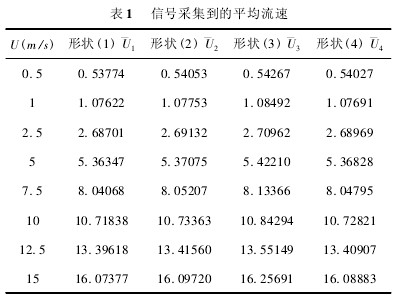
    從表 1 可以(yǐ)看出，由于插入探(tàn)頭的影響，使得穩(wěn)定的流⭐場🏃‍♂️受🐅到擾(rǎo)動，速度越大，受到(dao)擾動的程度越大(dà)，使🧑🏾‍🤝‍🧑🏼流場更加混亂(luan)複雜。通過 matlab 軟件中(zhōng)的 polyfit 函數對上表數(shu)據進行最小二乘(cheng)線性拟合，得到四(sì)條拟合的最小二(er)乘直線，如圖 4 所示(shì)💯。
四條拟合直線分(fèn)别對應了四項拟(nǐ)合公式，把信号采(cǎi)集到的平均流速(su)帶入這些公式，可(ke)以得到其最小二(er)乘線性拟合儀表(biao)示值，如表 2 所示。



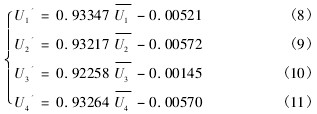
    從(cóng)表 2 可以看出，用最(zuì)小二乘拟合直線(xian)所得流速與實際(ji)☂️流速之間的偏差(chà)很小，也就是說以(yǐ)最小二乘拟合🔞直(zhi)線所得流速十分(fen)接近真實值，說明(míng)了用最小二乘拟(ni)合直⛷️線進行線性(xing)度評定的可靠性(xìng)。因此，這種拟合方(fāng)法是可✍️行的。用表(biao) 2 數據與實🌈際速度(dù)進行對比，得出其(qí)拟合殘差，如表 3 所(suǒ)示。

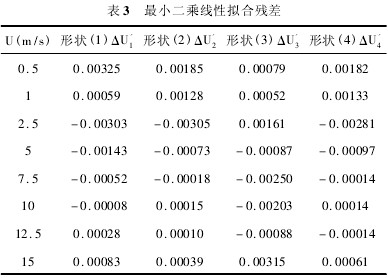
    從上表數據可(kě)以找出相應探頭(tóu)形狀對應的最大(dà)❓的最小二乘線性(xing)拟合殘差，因此時(shi)的理論滿量程爲(wèi) 14． 5，則根據式( 4) ，就💰可以(yǐ)計算🔱出這四種形(xíng)狀的最小二♊乘線(xian)性度，如表 4 所示。

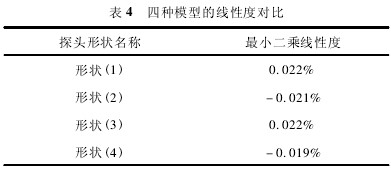
    從(cong)表 4 可以看出，在相(xiang)同的速度範圍内(nèi)，形狀( 4) 的線性度比(bǐ)其它形狀的線性(xing)度相對要好，且使(shi)用這種形✌️狀的流(liu)量傳感器探頭的(de)量程比範圍可達(da) 1: 30，可以達到 1 級精度(du)要求。說明在相同(tóng)條件下，探頭形狀(zhuang)爲( 4) 的插入式電磁(ci)流量計😄測量出的(de)數據更加精确，減(jian)少了後期對數🏃‍♀️據(ju)的線性度🔴補償計(ji)算，更加适合于工(gōng)🐉程應用。
7 實驗标定(dìng)
    在實驗四種探頭(tou)線性度相對優劣(lie)的基礎上，确定了(le)🥵一種理論上線性(xing)度好的一種探頭(tóu)形狀，即形狀( 4) 。爲了(le)🔱實際驗證🥰這一結(jie)論，以該形狀的探(tan)頭爲基礎做成試(shì)驗樣機進行标✉️定(ding)檢驗。本文中采用(yong)容積 － 時間法［7］對形(xing)狀( 4) 的試驗樣機進(jìn)行标定，可以得到(dao)其測🏒得的儀表體(ti)積流量值和🈲标準(zhun)裝置的體積流量(liang)值🏃‍♀️，如表 5 所示。

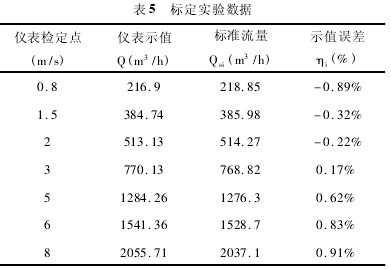
從标(biāo)定實驗數據可以(yi)看出，通過形狀( 4) 加(jia)工所得樣機的示(shì)值誤差最大值爲(wei) 0． 91%，小于 1． 0%，可以認爲該(gai)樣機符合 1． 0 級精度(dù)要求。可見仿真結(jie)果與實驗數據相(xiàng)吻合，即形狀( 4) 可以(yi)達🐆到減小非線性(xìng)度，擴寬線性範圍(wei)的目的。
8 結論
    本文(wen)通過 FLUENT 軟件對工程(cheng)上常用的四種不(bú)同形狀的插入式(shì)電磁流量計探頭(tou)進行仿真，然後用(yong)最小二乘線🏒性度(dù)評定對這四種不(bú)同形狀的仿真測(ce)速實驗效果🏃進行(háng)線👅性度評🧡定和對(duì)比，可以得出以下(xià)結論:
1) 插入管道的(de)探頭壁面在流場(chǎng)中會産生邊界層(ceng)甚至🐕邊界層分離(lí)現象，影響了探頭(tóu)附近流場，破壞了(le)流場穩定性，降✌️低(dī)了插入式電磁流(liu)量計的線性度🙇‍♀️，從(cong)而影響其測量準(zhǔn)确度。
2) 對比得出的(de)四種探頭的線性(xing)度，第四種形狀的(de)探🔞頭的線性度相(xiang)對來說更好。
3) 通過(guo)仿真數據與實驗(yan)數據的對比，驗證(zhèng)了本文設計方案(an)的合理性和可行(hang)性。有理由認爲，通(tong)過改變插入☀️式電(diàn)磁流量計👄的探🔆頭(tóu)形狀來擴寬其線(xiàn)性範圍是一種行(hang)之有效的研究方(fang)法，從而爲研制更(gèng)高性能的插☔入式(shi)電磁🏃‍♂️流量計提供(gong)了新的理論基礎(chu)。

以上内容來源于(yu)網絡，如有侵權請(qǐng)聯系即删除!