近年來，随着(zhe)流量計量行業的(de)發展， 電磁流量計(ji) 以其無可動部件(jian)、無壓力損失、測量(liang)量程範圍寬等優(you)點應用與各種場(chang)合，而在使用過程(cheng)中遇到的一個難(nán)題就是如何提高(gao) 大口徑大流量計(jì) 量的準确度。如果(guǒ)使用管道式電磁(ci)流量計測量大口(kou)徑管道流量，則其(qi)體積大、加工成本(běn)高并且标定📐和安(an)🚶裝維修都🏃🏻‍♂️十分🐅困(kùn)難，給工程應用帶(dai)來很多不💰便。所以(yi)在這種情況下，一(yi)般用插入式電磁(ci)流量計 代替管道(dao)式電磁流量計用(yòng)于測量大口徑管(guǎn)道的流量。
    但是插(cha)入式電磁流量計(ji)會産生非線性現(xiàn)象，影響測量⭐的準(zhǔn)确性。現在很多學(xue)者解決這個問題(ti)多采用的是多段(duan)非線性補償方法(fa)，把真個量程範圍(wei)裏面的流量分成(cheng)多個流量段，再✊分(fen)别求🔞解出不同階(jiē)🚶段的流量系數，從(cóng)而♉可以得出各個(ge)階段☂️的流量值。但(dàn)是這種方法使用(yong)起來比較複雜，且(qie)精度也受到了限(xian)制。所以🙇🏻本💋文從電(dian)磁流量計自身結(jie)構處罰，找出産生(shēng)非線性現象的原(yuan)因，從源頭上找出(chū)提高插入💜式電磁(ci)流量計線性度的(de)方法。
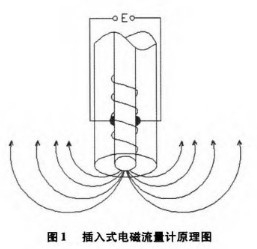
插入式電磁(ci)流量計工作原理(lǐ)
   插入式電磁流量(liàng)計測量原理是基(ji)于法拉第電磁感(gan)應定👨‍❤️‍👨律🌈E=BLν      其中，E爲兩(liang)電極之間産生的(de)感應電動勢，B爲磁(cí)✍️感應強度，L爲切割(ge)磁感應線的有效(xiào)長度，ν爲平均流速(sù)，流質爲導電介質(zhì)，原理如圖1所示。

并且(qie)（1）式經變換可表示(shi)爲
  當B和L都爲常數(shu)時，隻要測得感應(yīng)電動勢E就可以得(dé)到💔平均流速ν，因被(bèi)測管道的橫截面(mian)積已知，這樣就♌可(ke)以很容易求得某(mǒu)導電流質的體積(ji)流量。

其中，D爲被測(ce)管道内徑Qv爲體積(ji)流量。
  由（3）式可知，當(dang)插入管道結構一(yi)定時，體積流量Qv與(yu)比值E/B成正比，而與(yǔ)流體的溫度、密度(dù)、管内壓力等無關(guan)。當磁感應強度B爲(wei)常數時，體積流量(liàng)Qv與感應電動勢E成(cheng)正比，即體積流量(liàng)與感應電♊動勢之(zhī)🧑🏽‍🤝‍🧑🏻間是完全呈線性(xing)關系🧑🏽‍🤝‍🧑🏻的。
傳感器線(xiàn)性度評定
   線性度(du)是傳感器的主要(yào)靜态性能指标之(zhi)一，其定⭐義🌈爲測試(shi)系統的輸出和輸(shū)入系統能否想理(lǐ)想系統那天保持(chí)正常值🌈比例關系(xi)（線性關系）的一種(zhong)度量。線性度反應(yīng)了校準🐅曲線與某(mǒu)一規定直線一緻(zhì)的程度，詞規定直(zhi)線即爲按一㊙️定方(fāng)法确定的理想直(zhi)線。線性度又稱爲(wei)非線性度，參考GB/T18459-2001《傳(chuán)感器主要靜态性(xìng)能指标計算方法(fa)》中的線性度定義(yi)：正、反行程實際平(píng)均♌特性曲線相對(dui)于參比直線（拟合(he)直線）的最大偏差(chà)，用滿量程💋輸出的(de)百分比來表示。這(zhe)一指💞标通常以線(xian)性誤差表示

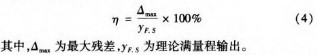
   本文(wen)采用最小二乘法(fa)進行線性度評定(dìng)，即拟合直線🈲爲最(zuì)小二🙇🏻乘直線。最小(xiao)二乘直線保證了(le)傳感器至極輸出(chu)的平均值對它的(de)偏差的平方和爲(wei)最小🛀，即可以保證(zheng)拟合直線得到的(de)結果與實測結果(guǒ)之間的偏差很小(xiao)，更具可靠性。根據(jù)定義，線性度即是(shi)校準曲線對🔅這條(tiao)最小二👣乘拟合直(zhi)線的偏離程度。

以(yǐ)上内容來源于網(wǎng)絡，如有侵權請聯(lián)系即删除!