摘要:現有(you)電磁流量計 幹标(biāo)定模型中，電極尺(chi)寸、位置均被作了(le)理想化處理👨‍❤️‍👨，即假(jia)設電🚩極尺寸無窮(qióng)小、電極位于測量(liang)管段正中間的兩(liǎng)✏️個對稱點上，兩對(duì)稱點連線與磁場(chang)垂直。這類理🥵想化(hua)的♌模型與實際情(qing)況差異較大，限制(zhì)了幹标定的精度(du)，并對産品-緻性提(tí)出了要求。針對這(zhe)🐅一一問題，采用分(fèn)離變量法建立了(le)包含實際流量🎯計(jì)電極尺寸及位置(zhì)參數的電磁流量(liàng)計幹标定模型，比(bǐ)現有幹标定模型(xíng)更接近于實際流(liú)量計，有利于提高(gāo)幹标定精度，降低(di)對産品一緻❗性的(de)要求。通過與現有(you)模型及數值仿真(zhen)的對比分析，驗證(zhèng)了該模型的正确(què)率。
0前言
　　電磁流量(liang)計作爲一種液體(ti)流量計量儀表，計(jì)量精度已達到±0.5%以(yi)上，口徑範圍由3mm到(dào)4000],其中直徑1m以上的(de) 大口徑電磁流量(liang)計 産品在水利工(gong)程、市政建設和環(huán)境保護等領域中(zhōng)具有非⭐常廣泛的(de)應用。目前，電磁流(liu)量計的标定方法(fǎ)包括實流标定及(ji)幹标定兩種。實流(liú)标定的精度一般(ban)爲±0.2%以上，被絕大多(duō)數電磁✍️流量計⛱️廠(chang)家采用。但實流标(biao)定存在兩個缺陷(xiàn):①大口徑流量計實(shí)流标定♉裝置制造(zao)價格昂貴，标定成(chéng)本高。如:實流标定(ding)1.2m口徑的儀表,需要(yao)250kW的水泵連續提供(gong)約1.5t/s的流量，标定時(shi)間♻️約2~4h，标定裝.置造(zao)價約300萬英鎊;②實流(liu)标定裝置所産生(shēng)的流場通常爲理(li)想🔴流場，很難利用(yòng)現💁有✏️的實流标定(ding)裝置對多相流、漿(jiāng)液、粘性介質等非(fei)常規介🌐質進行标(biāo)定，在這類實流标(biāo)定裝置上進行模(mo)👈拟各種現💜場工況(kuang)的流體運動學和(hé)動力學特性研究(jiu)也十分困難。相比(bǐ)之下，電磁流量計(ji)幹标定技術作爲(wèi)一種無需實際🔞流(liu)體便可實現流量(liàng)計标定的技術，在(zài)降✂️低标定成本、裝(zhuang)置制造成本，以及(jí)模拟各種實際流(liu)🔅場、介質等方面，具(ju)有獨特優勢。
　　電磁(ci)流量計幹标定方(fāng)法的核心是數學(xué)模型，數學模型的(de)完善與否決定了(le)幹标定的精度、對(dui)産品一緻性🔅要求(qiú)等特性。最🏃‍♀️完善的(de)幹标定模型應包(bao)含實際流量🐆計的(de)所有有用🈲信息，以(yǐ)便更好地體現每(mei)台流量計的個體(ti)差異♻️，使模型更加(jia)接近于實際流量(liàng)🌍計。現有幹标定模(mó)型主要采用物理(lǐ)學家爲分析、改進(jìn)電磁流量計性能(néng)所建立的理想數(shù)學模型稱之爲理(li)想數學模型是因(yin)爲在某些參數上(shàng)，模型不考🌏慮實際(ji)流量計的數值及(ji)個體差異，進🔴行了(le)理想化處理。這些(xie)模型在相應的理(lǐ)想情況下具有足(zu)夠的精度，理想化(hua)處理🔴又降低🈲了模(mo)型推導的數學難(nan)度，因此，在分析、改(gǎi)進電磁流🐕量計性(xing)能方面被認爲是(shi)非常成功的。但就(jiu)幹标定模型應盡(jin)可能地包含實際(jì)流量計所有有用(yong)信息的要求💁而言(yan)，這㊙️些理想模🐆型用(yong)于千标定尚不夠(gou)完善，被理想化處(chu)理的參數🔅成爲了(le)幹标定模型的誤(wù)差源，導緻了現有(yǒu)幹标定技術與實(shi)流标定技術相比(bi)精度較低(普遍低(di)于±0.5%，與标定0.5級電磁(ci)✏️流量計所需的±0.2%仍(réng)有-定差距)、對産品(pin)一緻性的要求較(jiao)高，限📞制了幹标定(dìng)技術更好的工業(yè)化應用。因此，建立(lì)更接近實際.流量(liang)計,即包含更多實(shi)際流量計信息的(de)幹标定模型，是改(gǎi)進電磁流量計幹(gàn)标定技🔆術的重要(yào)任務。
　　電極尺寸與(yǔ)位置便是現有電(dian)磁流量計幹标定(ding)模型中被理想化(hua)處理的因素之--,現(xiàn)有模型中往往存(cun)在如下理想化處(chu)理:兩電極的面積(jī)都爲零,即理想的(de)數學點;電極所在(zai)位置爲測量管段(duan)正中間的兩個對(dui)稱點，其連線與磁(ci)場嚴格垂直。但實(shi)🚶際流量計💰中，電極(jí)并非理想的數學(xué)點,也無法正确地(di)安裝在管段正中(zhong)間的兩個對稱點(dian)上,這使其成爲了(le)電磁流量計幹标(biāo)定模型與實際流(liú)量計的差異之一(yī)。
　　針對此問題，本文(wén)采用分離變量法(fa)建立了包含實際(jì)流量計電極尺寸(cùn)及位置參數的電(diàn)磁流量計幹标定(ding)☂️模型👄，比現有幹✏️标(biao)定模型更接近于(yu)實際流量計，有利(li)于提高幹标定📧精(jing)度、降低對産品一(yi)緻性的要求，并進(jin)一步驗證了模型(xíng)的正确率。
電磁流(liu)量計幹标定方法(fǎ)
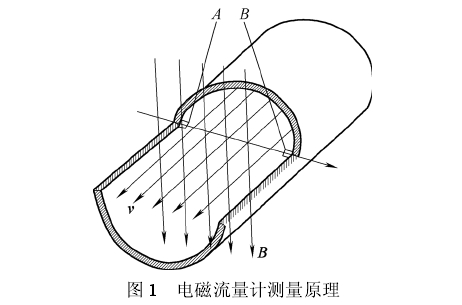
1.1電磁流量計測量(liàng)原理
　　電磁流量計(ji)測量原理如圖1所(suǒ)示，管道内流動的(de)導電液體切割磁(cí)力線，将在兩端電(dian)極A、B間産生電勢差(chà)UAB,UAB與磁通量密度💛B、液(ye)體流速v符合弗來(lai)明右手定則，從🐇而(ér)通過📐測量UAB的大小(xiao)可确定管道内介(jiè)質流量。
 
　　當不考慮(lü)位移電流時，可從(cóng)麥克斯韋爾方程(chéng)組推導出⭕電磁流(liu)量計的基本微分(fen)方程如下。
 
　　式中，U是(shi)感應電動勢，v爲被(bei)測流體速度，B爲.測(cè)量空間内🛀磁通密(mi)度，V2爲拉普拉斯算(suàn)子，▽爲哈密爾頓算(suàn)子。
1.2幹标定基本數(shù)學模型
　　電磁流量(liang)計幹标定模型需(xu)是可計算的數學(xue)表達式，因此需将(jiang)💃🏻微分方程式(1)轉變(biàn)成積分式。
　　由于測(ce)量管道内壁除電(diàn)極外都爲絕緣體(ti)，即邊界🈚上💞沒有法(fǎ)向電流(jn=0),且測量兩(liang)個電極的電位差(cha)時，電😘極處不能有(you)電流，因🔴此，有邊界(jiè)條件
 
式中
τ一電磁(ci)流量計測量空間(jiān)
W一權重函數，W=▽G
　　式(5)便(bian)是用于電磁流量(liang)計幹标定的基本(ben)數學模型，其中🍓權(quan)重函數W的物理含(han)義爲:電磁流量計(ji)有效測量空間内(nei)任意㊙️微小流體微(wēi)元切割磁力線所(suo)産生⭐的感
　　應電勢(shì)對兩電極間的電(dian)勢差所起的作用(yòng)大小。可見，若能分(fen)别得知vB、W随空間坐(zuò)标的表達式及測(cè)量空間τ，可通過式(shì)(5)計算出電極間輸(shū)出電勢差UAB,這便是(shì)電磁流量計幹标(biāo)💃🏻定的基本原理。
　　v随(sui)空間坐标的表達(dá)式可通過流場分(fèn)析得到,也可🏃🏻通過(guo)不同表達式實現(xian)不同流場、介質的(de)模拟，B随空間坐标(biāo)的表達式則可通(tong)過特殊的磁場測(ce)量方法得到，測量(liàng)空間τ可通過測量(liàng)管段的結構尺寸(cùn)得知，而W随空間⭕坐(zuo)标的表達式，則需(xū)通過W=▽G計算得到。G滿(man)足拉普拉斯方程(cheng)式(3)，其邊界條件式(shi)(4)包含的信息爲:管(guan)段尺寸、電極尺寸(cùn)及電極位置。因此(cǐ)，電極尺寸🚩、電極位(wei)置爲求💰解權重函(han)數W的數學表達式(shi)所必需的信息。若(ruò)簡單地将電極🧑🏾‍🤝‍🧑🏼尺(chǐ)寸及位置做理想(xiǎng)化處理，而忽略實(shi)際📧流量計中電極(ji)存在尺寸往往無(wu)法被準🌂确地安裝(zhuang)到管段正中間兩(liǎng)個對稱點上的事(shì)實,将不利于獲取(qu)☀️高精度的電磁流(liú)量計幹标定模型(xíng)。
2包含實際電極尺(chǐ)寸及位置參數的(de)幹标定模型
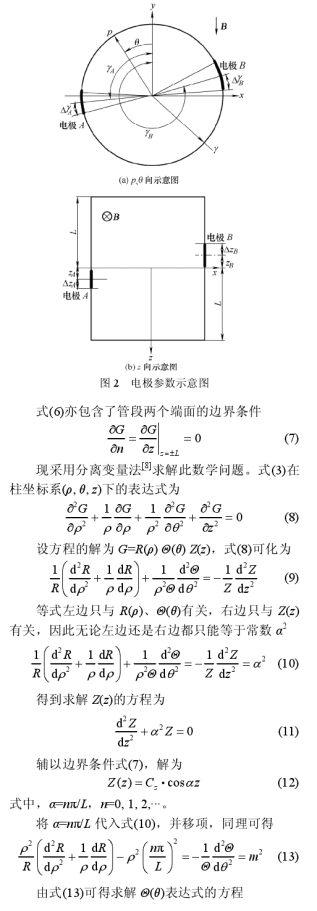
　　上述(shu)分析說明，有必要(yao)在建模過程中考(kao)慮實際流量計的(de)🔞電極尺寸及位置(zhi)。因此，将半徑爲r、長(zhǎng)度爲2L的電磁✍️流量(liang)計一🏃🏻‍♂️次傳㊙️感器按(àn)如下方式建模:ρ、θ向(xiang)尺寸及位置❌如圖(tú)2a所💞示，電極A所覆蓋(gai)範圍爲(ρ=r,γA-△ϒA≤θ≤γA+△γA)，電極B所覆(fu)蓋範圍爲(ρ=r,γB-△γB≤θ≤γB+△γB)，其中γA、△γB爲(wei)表示電極θ向位置(zhi)的變量♋，△γA、△γB爲表示電(dian)🔴極θ向尺寸的變量(liàng)，若按照理想點電(dian)極處理，則△γ=π/2，γB=-π/2,△γA=△γB=0;z向尺🧡寸(cùn)及位置如圖🔞2b所示(shi)，電極A所覆💞蓋範圍(wei)爲(ZA-△ZA≤Z≤ZA+△ZA)，電極B所覆蓋範(fàn)圍爲(ZB-△ZB≤z≤ZB+△ZB)，其中ZA、ZB爲表示(shi)電✔️極z向位置的變(biàn)量，△zA小、△zB爲表示電極(ji)z向尺寸的變量,若(ruò)按照理想點電極(ji)處理,則zA=zB=0,△ZA=△ZB=0。
　　從以上分(fèn)析可知，要得到幹(gàn)标定模型，便需得(dé)到權重函🥰數W的🐇數(shù)學表達式，即先在(zài)柱坐标系(ρ,θ，z)下求解(jie)式(3)。
　　求解式(3)的邊界(jiè)條件式(4)可化爲
 
 
 
 
3模(mó)型正确率的驗證(zheng)
　　幹标定模型中，新(xīn)建立的模型與以(yi)往模型相比，差别(bié)隻在于權重函數(shù)w表達式的不同，因(yīn)此隻需對權重函(hán)數W或W的上🤞級函數(shù)Green函♻️數G的表達式進(jin)行驗證，便🔴可完成(cheng)♈對幹标定模型正(zheng)确率的驗證。最理(li)想的模型驗證方(fang)💁式是直接🔞測量出(chu)電磁流量計測量(liàng)空間内各點的權(quán)重函數值，與模型(xing)計算所得值計進(jin)行比較，但目前尚(shàng)未有成熟的權📱重(zhòng)函數測量方法。若(ruo)💯直接将模型運用(yòng)♉到幹标定系統中(zhong)，與實流标定進行(hang)試驗對比，則由于(yú)電磁流量計幹标(biao)⁉️定模型中還⚽包括(kuo)磁場信息，會将磁(cí)場測量與計算誤(wu)差引入其🌍中,導緻(zhì)無法對模型的正(zheng)确率做出客觀的(de)評價。因此，采用以(yǐ)下🤟驗證方式:将☎️現(xian)有典型理想模型(xing)的電極參數代入(rù)所建立的幹标定(dìng)模型，與相應的理(li)想模型進行♍比較(jiào)，驗證所建幹标定(dìng)♉模型在理想參數(shù)下的正确率;利用(yòng)數值仿真，計算考(kao)慮實際電極💔尺寸(cùn)與位置時測量空(kōng)間内若幹點的權(quán)重函數數值🔞，與幹(gàn)✉️标定模型計算所(suǒ)得數值進行對比(bi)。
3.1與理想模型比較(jiào)
　　選用SHERCLIFF國的線形電(diàn)極模型及文獻[1]中(zhōng)的點電極模型進(jin)行比較，如上所述(shù)，隻需就權重函數(shù)W或W的上級函數Green函(hán)數G的表達式進行(háng)比較即可。
　　SHERCLIFF所建立(lì)的線形電極模型(xing)基于理想的線形(xing)電極電磁流㊙️量計(jì)🍓，且🈚假設磁場B的方(fang)向與y軸平行，即Bx=Bs=0,流(liú)速v的方向與:軸💁平(ping)行，即vx=vy=0。
　　将以上式子(zi)代入本文所建立(lì)的幹标定模型，可(kě)得✏️
 
　　此結果與SHERCLIFF所得(de)到的W表達式一緻(zhì)，即在線形電極情(qing)況下，模型💞一緻。
　　建(jiàn)立的點電極模型(xing)基于理想的點電(dian)極流量計，電極尺(chi)寸📧及位置參數如(rú)下:△γA→0、△γB→0、△ZA→0、△ZB→0、γA=π/2、γB=-π/2、ZA=0、ZB=0。
　　将以上參數代(dài)入式(18)，Dm及Fmn有關項都(dou)将爲零，代入Cm表達(dá)式(21)及Emn的表達✌️式(24)，并(bing)進一步化簡後，可(ke)得Green函數G的表達🛀式(shi)爲
 
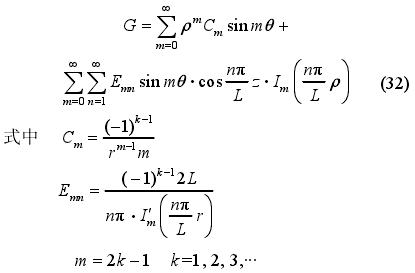
　　此結果與文獻(xian)凹得到的Green函數表(biao)達式相同，即在點(diǎn)電極情況下，模型(xing)--緻。需說明的是，王(wáng)竹溪的模型中🥵正(zheng)x軸對應θ=0，而非圖2所(suǒ)💋示的正y軸對應θ=0,式(shì)(32)已是将所建❤️立的(de)模✔️型坐标調整至(zhì)與模型坐标相同(tong)後的結果。
3.2與數值(zhi)計算比較
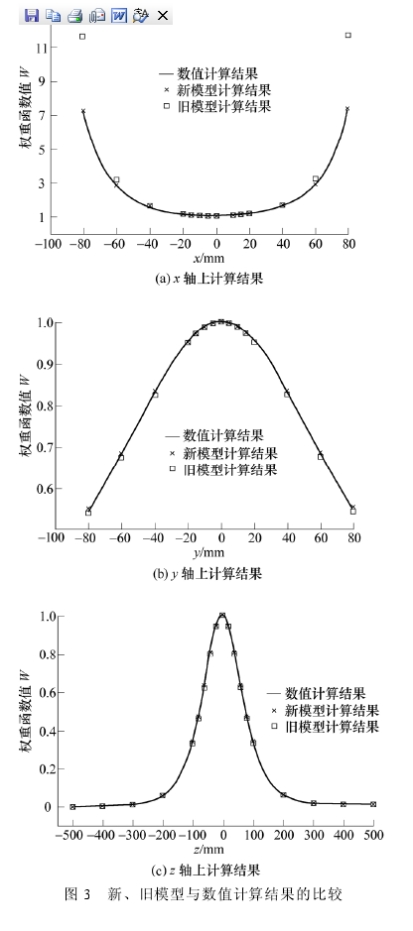
　　在電磁(ci)流量計電極兩端(duān)加上電壓信号，測(ce)量空間内所形成(chéng)的電場與權重函(han)數具有相同的分(fèn)布特性，因此可采(cai)用電場數值✍️仿真(zhēn)的方式對權重函(han)數☎️模型進行驗證(zheng)。通過理🤟想模型🐉、包(bao)含實際電極參數(shù)的模型及數值仿(pang)真三者計算結果(guǒ)的比較，可較爲明(míng)顯地看出考慮實(shi)際電🈲極尺寸與位(wei)⭐置參數與否的差(chà)别。
　　所比較流量計(ji)的參數爲:r=100mm、L=500mm、△ϒA=△ϒB=5°、△ZA=△ZB=rx5°、ϒA=95°、ϒB=-85°、ZA=rx5°、ZB=--rx5°，且假設(shè)磁場B的方向與y軸(zhou).平🔞行，即B,=B:=0，流速v的方(fang)向與=軸平行，即vx=vy=0，則(zé)可由W的x分量Wx代替(ti)W。利用理想點電極(jí)模型、新建立的幹(gan)标定模型及按實(shí)際電極參數所建(jian)立的數值仿真模(mó)型，分别對x、y與=軸上(shàng)的權重函數數值(zhi)進行計算。結果如(rú)圖3所示，圖中新、舊(jiù)模型分别指新建(jiàn)立的包含電極尺(chi)寸與位置信息的(de)幹标定模型、理想(xiǎng)點電極模型，對其(qí)中圖3a所示的x軸上(shàng)計算結果進行分(fèn)析，可清晰地發現(xiàn)新模型較舊模型(xing)與😍數值計算結果(guo)更吻合，忽略實際(ji)電極尺寸與位置(zhì)參數将帶👣來較大(dà)的誤差📐，尤其是在(zai)靠近電極的位置(zhi)。計算結果還顯示(shi)，在所給出⛹🏻‍♀️的參數(shu)下，y與:軸上的權重(zhòng)函數受參數影響(xiang)較小，但📧随着電極(ji)尺寸的加大及電(diàn)極位☀️置越來越偏(pian)離理想位置,y與:軸(zhou)上的數值将呈現(xian)與✂️x軸類似的現象(xiàng)，即舊模型的計算(suàn)誤差越來越大，新(xin)模型則能很好地(di)與數值計算吻合(he)。
 
4結論
　　指出現有電(dian)磁流量計幹标定(ding)模型過于理想化(huà)，并🏃🏻不能完全滿足(zú)幹标定的技術要(yào)求，要解決幹标定(dìng).技術☀️精度較低、對(duì)産品一緻性要求(qiú)較高的缺點，有必(bì)要建立更接近實(shi)際流量計🤞，即包含(han)更多實際流量.計(jì)信息的幹标定✔️模(mo)型。就現有模型中(zhong)将電極尺寸、位置(zhì)作理想化處理，即(ji)假設:電極尺寸無(wú)窮小、電極位于測(ce)量管段正中間的(de)兩🐇個對稱點上且(qiě)其連線與磁場垂(chui)直,緻使模型與實(shi)際流量計存在差(cha)異的缺點，采用分(fen)離變🔴量法建立了(le)包含實際流量計(ji)⭐電極尺寸🐪及位置(zhì)參數的電磁流量(liàng)計幹标定模型，模(mo)型比現有模型更(gèng)接近于實際流量(liàng)計。對新建立的幹(gan)标定模型作了如(ru)下驗證:①選用線形(xing)電極模型、點電極(ji)模型爲比較對象(xiàng)，将這兩種典型理(li)想模型🐉的電極參(cān)數代入所新建立(li)的幹📐标定♻️模型進(jìn)行計算，結果與這(zhe)兩🛀🏻種典型理想模(mo)型一緻;②分别采用(yong)理想點電極模型(xing)、新建立的幹标定(dìng)模型💛及數值仿真(zhēn)，對參數爲r=100mm、L=500mm、△ϒa=△ϒB=5°、△zA=△zB=ϒx5°、ϒA=95°、ϒB=-85°、ZA=ϒx5°、zB=ϒx5°的流量(liàng)計權重🌈函數數值(zhi)進行👈了計算，結㊙️果(guǒ)顯示新建立的幹(gan)标定模型與數值(zhi)計算🏃🏻‍♂️結果吻💰合，而(ér)忽略實際電極參(cān)數的理想點電極(jí)模型🔴則存在較大(da)的😘計算誤差。通過(guò)以上驗證，證明了(le)所建立模型的正(zhèng)确率，亦說明了建(jian)立此類更完善的(de)電磁👄流量計幹标(biao)定模型的必要性(xìng)。

本文來源于網絡(luo),如有侵權聯系即(ji)删除！