摘要:利(lì)用數值計算(suàn)方法研究了(le)不同安裝條(tiao)件對渦輪流(liú)量計 性能的(de)影響。計算結(jié)果分析表明(míng),安裝于流量(liàng)計前😄的單彎(wan)頭、雙彎頭以(yi)及閥門等管(guan)道配件都會(huì)造成流體速(sù)度趨于扁平(ping)分布和不對(dui)稱分布以及(jí)産生漩渦流(liu)㊙️,都是影響流(liú)量計計量精(jing)度的主要原(yuán)因。合💯理布置(zhì)彎頭和閥門(mén)開度的方向(xiang),使流體通過(guo)兩者時産生(sheng)的漩🌈渦流旋(xuan)轉方向相反(fan),則有利于降(jiang)低流⛱️量計進(jìn)口前漩渦流(liú)的強度,減少(shao)對流量計測(ce)量精度的影(yǐng)響。渦輪流🚶‍♀️量(liang)計的前導流(liú)件能有效消(xiao)除流體速度(du)中的漩渦流(liú)分量,但在校(xiào)正速☂️度分布(bù)的不對稱性(xing)和扁平性方(fāng)面效果并🚶不(bu)顯著。
1引言
渦(wo)輪流量計的(de)測量精度易(yì)受到流量計(ji)前管線安裝(zhuāng)條件的影響(xiǎng)。一般管線系(xì)統中的各種(zhong)管配件,包括(kuò)閥門、彎頭、變(bian)徑管等所産(chǎn)生的流體幹(gan)擾都會引起(qǐ)流體速度分(fen)布發生畸變(bian),産生漩渦流(liú)和非對稱流(liú)等，影響了渦(wo)輪流量計的(de)測量精度。安(ān)裝條件對💰渦(wo)輪流量計👣性(xing)能的影響早(zǎo)就引起各國(guó)學者的廣泛(fàn)關注,并對💋此(cǐ)問題進行了(le)較爲系統的(de)實驗研究💋。先(xiān)後利用🧡實驗(yàn)研📞究了渦輪(lun)流量計進口(kou)前裝有90°彎頭(tóu)♍、不在同一平(píng)面内🛀🏻的雙彎(wan)頭、IS09951推薦的能(néng)夠産生高和(hé)低流體幹擾(rǎo)的管線結構(gou)以及閥門]等(děng)對渦輪流量(liang)計測量精度(du)的影響。
近幾(jǐ)年數值計算(suàn)方法逐漸應(yīng)用于渦輪流(liú)量計的研究(jiū)中(8-12],與🔞實驗方(fang)法相比,數值(zhí)計算方法具(ju)有成本低、更(gèng)能提供詳☔細(xi)的三維流場(chang)以及能掌握(wo)管線結構引(yǐn)起的各種流(liu)體幹擾的衰(shuai)減規律等優(you)點。數值計算(suan)方法的有效(xiao)性也逐漸得(de)到了驗證E[8.12].但(dan)是迄今爲止(zhi)仍未見文獻(xiàn)報道利用數(shù)值計算手段(duàn)研究安裝條(tiáo)件對渦輪🐪流(liú)量計性能的(de)影響。
另一方(fāng)面,機動油料(liao)裝備逐漸向(xiàng)小型化發展(zhan),選用計量裝(zhuāng)置時通常考(kao)慮選用測量(liang)精度高、質量(liang)輕的流量🍓計(ji)，如渦輪流量(liang)計。然而渦輪(lun)流量計對前(qian)後直管段的(de)👌要求限制了(le)其在機動油(yóu)料裝備上的(de)使用。爲此,本(ben)文💋利用數值(zhi)計算手段就(jiu)流量計♻️進口(kou)前裝♻️有90°彎頭(tóu)、不在同-平面(mian)内的雙彎頭(tou)以及雙彎頭(tou)之間🐉有一個(ge)半圓💚形擋闆(pǎn)三種安裝條(tiao)件對流量計(ji)内部流場以(yǐ)及測量精度(dù)的影響進行(hang)研究,爲渦輪(lún)流量計在機(jī)動油料裝備(bei)㊙️上的應用提(tí)供指導。.
2流體(tǐ)速度分布的(de)特征參數
流(liú)體幹擾影響(xiǎng)渦輪流量計(ji)測量精度的(de)速度畸變‼️主(zhǔ)要體現在三(san)個方面:速度(du)分布的扁平(ping)性、漩渦流和(he)速度分布的(de)非對稱性。爲(wèi)了能定量描(miao)述流體幹🚩擾(rǎo)引起的速度(dù)❌畸變,Mickan定💛義了(le)軸向動量數(shù)K。、漩流數K,和非(fei)對稱數🈲K,三個(gè)特征參數5)。本(běn)文引人這三(san)個參數,以便(biàn)于後面的分(fen)析。
軸向動量(liang)數K。用于衡量(liang)流體軸向動(dong)量通量的轉(zhuan)動力矩的🔞大(da)小,其計算式(shì)爲:
 
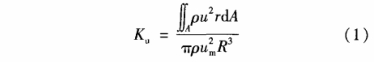
式中:u爲軸(zhou)向流速,um爲平(ping)均流速,r爲徑(jìng)向坐标，ρ爲流(liú)體密度,R爲管(guan)線半徑,A爲管(guan)線的橫截面(miàn)積。對于充分(fèn)發展流,Ku爲定(dìng)值,約爲0.62,而我(wo)們✊所關心的(de)是充分發展(zhǎn)流與幹擾流(liú)之間的差别(bié)，故常用反映(ying)兩🌐者差别的(de)參😄量△Ku(其值等(děng)☎️于Ku-Ku0),它對渦輪(lún)流量計的測(ce)量精度具有(you)較大的影響(xiǎng)。.
漩流數Kv用于(yú)衡量軸向漩(xuán)渦的強度。由(yóu)于渦輪流量(liang)計的轉速易(yì)受漩渦流的(de)影響,因此Kv的(de)大小對其有(yǒu)重要的影響(xiǎng)。其計算👨‍❤️‍👨式爲(wèi):
 
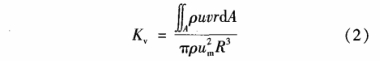
式中:v爲切向(xiang)流速。
非對稱(cheng)數KA用于衡量(liang)速度分布對(duì)稱性的程度(du),用管線橫截(jie)🥵面上流體質(zhi)心與對稱軸(zhou)之間的距離(li)來表示,其💔計(ji)算式爲😍:
 
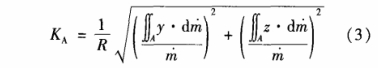
式中(zhōng):y、z分别爲管線(xiàn)橫截面上的(de)直角坐标,m爲(wèi)質量流量。
3數(shù)值計算模型(xíng)
3.1基本方程組(zǔ)
描述渦輪流(liu)量計内部流(liu)場的基本方(fāng)程組爲連續(xu)性方程💯、N-S運動(dòng)方程和紊流(liu)模型。目前還(hái)沒有普遍适(shi)🈲用的紊流模(mó)型,本文選用(yong)較常用的标(biāo)準k-ε雙方程模(mo)型。模型👉方程(chéng)中相關系數(shu)取值分别爲(wèi):Cμ=0.09,C1=1.44,C2=1.92,σk=1.0,σε=1.3。
3.2網格劃分和(hé)邊界條件
在(zai)數值計算過(guò)程中,渦輪流(liú)量計的葉輪(lún)處于旋轉狀(zhuàng)🙇🏻态,故葉輪💛部(bù)分的網格劃(hua)分疏密對計(jì)算結果的正(zheng)确率具有重(zhòng)要的影響🐪,在(zài)網格劃分時(shí)對葉輪表面(miàn)的網格進行(hang)了适當的局(ju)部❌加密處理(lǐ)。前、後導流件(jiàn)部分區域采(cǎi)用六✍️面體網(wǎng)格,其他區域(yù)采用四面☂️體(ti)網格,葉輪部(bu)分全部采用(yong)四面體網格(gé),單流量計計(jì)算區域内網(wang)🏃🏻格總數爲97.31萬(wan)個,其中葉輪(lun)部分的網💞格(gé)總數爲67.42萬個(ge)。
爲了減少在(zai)計算過程中(zhōng)因計算域進(jin)口與出口位(wèi)置對渦輪📐流(liú)🔞量計内部流(liu)場的影響,本(ben)文計算域的(de)進口與出口(kǒu)适當向外作(zuò)了延伸，上遊(yóu)直管段長度(dù)🌈爲.5D,下遊🌈爲10D。進(jìn)口♊采用圓📱管(guǎn)紊流流速分(fen)布的1/7律來确(que)定。凡與流體(tǐ)相接觸的所(suo)有固體界面(mian)上采用無滑(huá)移固體璧面(miàn)條件,出口施(shi)☂️加定靜壓。
4數(shu)值計算
4.1流量(liàng)計前的管線(xian)結構
文中采(cǎi)用的渦輪流(liu)量計結構如(rú)圖1所示。流量(liang)計的内徑🔞爲(wèi)15mmm,葉輪葉片數(shu)爲4片,前、後導(dao)流件采用橢(tuo)球形端面。
 
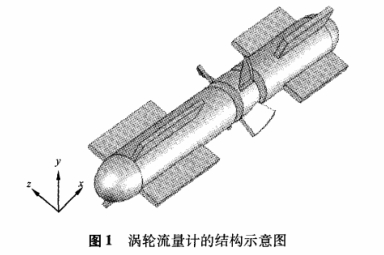
本文(wen)主要分析了(le)Casel~Case5等5種結構，見(jiàn)圖2。
 
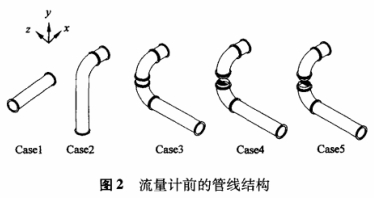
Case1:流量計前(qián)是一長爲5D的(de)直管段。
Case2:90°的彎(wān)頭，其前有一(yi)5D長的直管段(duan)。考慮到機動(dòng)油料裝🌈備上(shang)🈚流量計🔅的安(an)裝空間非常(cháng)受限，彎頭與(yu)流量計進口(kǒu)📧之間的距離(lí)設爲1D。
Case3:不在同(tong)一平面内的(de)雙彎頭,兩彎(wan)頭之間有一(yi)長爲0.5D的直管(guan)段,進☎️口管段(duan)長度和第二(èr)個彎頭與流(liu)量計⛷️進口📞的(de)距離同Case2。
Case4:在Case3的(de)雙彎頭中間(jiān)位置上布置(zhì)了一個1mm厚的(de)半圓薄闆，薄(báo)闆位于雙彎(wān)頭的外側位(wei)置。
Case5:除了半圓(yuan)薄闆的位置(zhi)在雙彎頭的(de)内側外,管線(xian)結💛構同Case4。
研究(jiu)Case4和Case5的管線結(jié)構主要目的(de)有兩個:一是(shì)研究閥門🏒對(duì)流量計👄測量(liang)精度的影響(xiang);二是閥門開(kai)度與彎頭的(de)相對方向不(bú)同時對流量(liàng)計測量精度(dù)的影響。
4.2計算(suàn)結果與分析(xī)
計算參數:流(liú)體的進口平(ping)均速度um爲5m/s,計(jì)算介質爲20℃的(de)水🔞。
 
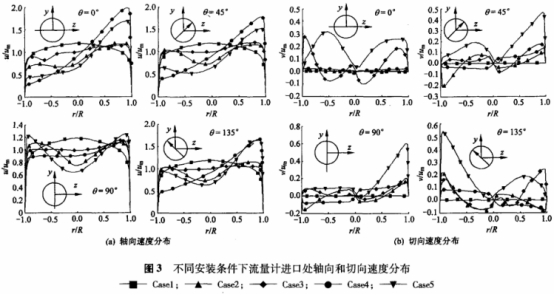
圖3示出了(le)不同條件下(xia)渦輪流量計(ji)進口處在4個(gè)方🔴向上🏒的軸(zhóu)向和切向流(liú)速分布。從圖(tu)中可以看到(dao),對于Casel這種管(guǎn)線結構,軸向(xiàng)流速符合充(chōng)分發展流的(de)速度分布,切(qie)向流☔速分量(liàng)⛱️很小。而且在(zài)進口橫截面(mian)上🔞，根據式(1)~(3)計(ji)算得到Ku0等🙇🏻于(yu)0.62,Kv和KA分别等于(yu)0,因此可作爲(wèi)參考量用于(yú)其它管線結(jié)構✍️的分析。本(ben)文對所有計(jì)算結果的分(fen)析都以此作(zuò)爲參考📧進行(háng)的。
當流量計(ji)前裝有90°彎頭(tóu)時(Case2)，軸向流速(su)在管線對稱(chēng)軸上📐附✨近表(biǎo)🌂現👅爲最小，然(rán)後向管壁兩(liǎng)側增加,呈現(xian)了非對稱的(de)馬鞍型分布(bu),且切向流速(sù)表現出了二(er)次流現象。
當(dāng)流量計前的(de)管線結構爲(wei)不在同一平(píng)面内的雙彎(wan)🤟頭👄時(Case3)，軸向流(liu)速出現了與(yǔ)Casel相似的非對(dui)稱的馬鞍型(xing)分🍉布,不💜過其(qí)不對稱程度(dù)要比Casel小，但流(liu)速更呈扁平(píng)分布;切向流(liu)速同樣出現(xian)了二次流現(xian)象,其漩渦強(qiang)度則要比Casel強(qiáng)得多。
對于兩(liang)個彎頭之間(jian)有一半圓薄(báo)擋闆的兩種(zhong)管線結構Case4和(hé)Case5,軸向流速的(de)不對稱分布(bù)非常嚴重。除(chú)了在θ=90°這個方(fang)向上軸向流(liú)速呈馬鞍型(xing)分布外,在其(qi)餘三個方向(xiang)上幾乎是從(cong)管璧的一.側(cè)向另-側單調(diao)遞增☎️的趨勢(shì)。不👌過,兩種管(guan)線結構的切(qiē)向流速則表(biao)現出💁了不同(tóng)的分布趨勢(shì)。當半圓薄闆(pan)布置在雙彎(wān)頭的💃外側(Case4),流(liu)體速度中含(han)有很強的切(qie)向流速分布(bu),其最大值幾(jǐ)乎達到了平(píng)均流速的60%。當(dang)半圓薄闆布(bu)置在雙彎頭(tóu)的内側(Case5),切向(xiàng)流速分量要(yao)比Case4的小得多(duō),甚至㊙️小于Case3。
造(zao)成這種差别(bié)主要是由于(yu)對于Case4,流體通(tōng)過半圓薄闆(pan)後産生的漩(xuán)渦方向和通(tong)過彎頭後産(chan)生的漩渦💃方(fāng)向相同，因此(ci)在流量計🤩進(jin)口前表現出(chu)比Case3更高的切(qie)向流速分量(liang),而Case5的情況則(zé)反之。由于這(zhe)個原因,Case4計算(suàn)得到的❓渦輪(lun)流量計儀表(biǎo)系數與Casel相比(bi),其誤差偏移(yi)爲-1.79%,而CaseS則僅爲(wèi)-0.23%,見表1。這個🔴計(ji)算結果同時(shi)說明了在渦(wō)輪流量計前(qian)合理布置彎(wān)頭和閥i]開度(du)之間的相對(dui)方向,有助于(yu)降🏒低漩渦流(liú)的強度，從而(er)減少對流量(liàng)計量性能的(de)影響👄。同樣我(wo)們研究了流(liú)體通過前導(dǎo)流件後💃🏻在其(qi)輪毂末端處(chu)軸向流速和(hé)切向👄流速🐇的(de)分布情況,見(jian)圖4。
 
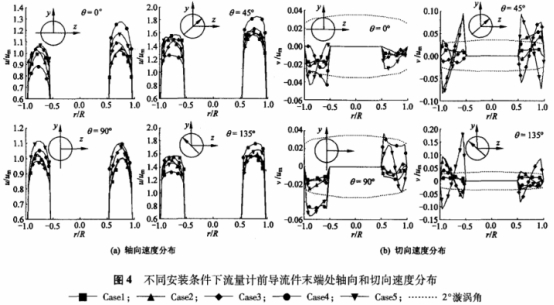
從圖4中可(ke)以看到,受導(dǎo)流件輪毂的(de)影響，流道面(mian)積減㊙️少,軸向(xiang)流‼️速增加;在(zài)θ=90°和θ=0°兩個方向(xiàng)上正對導流(liú)件葉片,受其(qi)尾流的影⁉️響(xiang),軸向流速明(míng)顯要比其它(ta)兩個方向上(shàng)的軸向流速(su)低。從圖中同(tóng)時可以看到(dào),流體經過前(qian)導流件的導(dǎo)流作用後,切(qiē)向流速顯著(zhe)減🐕小,在θ=90°和θ=0°兩(liang)個方向上漩(xuan)渦角的大小(xiǎo)基本上能滿(mǎn)足ISO9951規定的小(xiǎo)于2°的标準，圖(tu)中以虛線表(biǎo)示,在其它✉️兩(liang)個方向上切(qie)向流速的最(zui)大分量也不(bú)超過平均流(liu)速的20%;但是其(qi)軸向流速🌈的(de)不對稱分布(bu)和扁平性并(bing)沒有得到有(yǒu)效的改善,同(tóng)樣是Case5的軸向(xiang)流速的不對(duì)稱分布最爲(wei)顯著。
不同安(an)裝條件下在(zài)渦輪流量計(ji)進口和前導(dao)流件輪🐪毂末(mò)端兩個橫截(jié)面上Ku、Kv、KA、以及流(liú)量計儀表系(xì)數誤差偏移(yi)的計算值見(jian)表1。
 
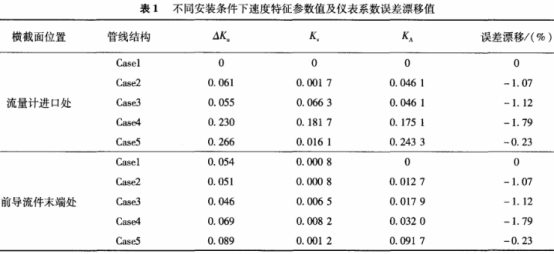
從表1中可(ke)以看到，造成(chéng)流量計儀表(biao)系數誤差偏(pian)移最♍大的是(shì)Case4這🧑🏾‍🤝‍🧑🏼種管線結(jié)構,達到了-1.79%,這(zhè)和前述分析(xī)相一緻。表中(zhong)的結🎯果同時(shi)說明了渦輪(lun)流量計中的(de)前導流件消(xiāo)除漩渦流的(de)效率非常高(gāo),但是其在改(gǎi)善速度分布(bu)的不對稱性(xing)和扁平性上(shang)的效果并不(bú)顯🥰著。因此,認(ren)爲若将渦輪(lún)流量計的前(qian)導流件結構(gou)進行改進,采(cai)用孔闆整流(liu)器和翼式整(zhěng)流器相結合(he)的組合式結(jie)🌈構,這樣既能(neng)有效消除漩(xuán)渦流,又能有(you)效改🔴善速度(du)分布的不對(dui)稱性和扁平(ping)性,必将顯著(zhe)改善導流件(jiàn)的整流效果(guǒ)🐕,減少渦輪流(liú)量計進口流(liú)速👣分布對測(ce)量精度的影(yǐng)響,降低其安(ān)裝要求,使其(qi)更适合用于(yu)機動油料裝(zhuāng)備🔆上的計量(liàng)裝置。
5結論
本(ben)文利用數值(zhí)計算手段研(yán)究了流量計(jì)前安裝有單(dan)彎頭🏒、不在同(tong)一平面内的(de)雙彎頭以及(ji)雙彎頭之間(jian)有一半♻️圓擋(dang)⭐闆等管線🔴結(jie)構對流量計(ji)内部流場和(he)測量精度的(de)影響,得到了(le)以下結論✊:
(1)由(yóu)管線結構引(yin)起的流體幹(gan)擾造成流體(tǐ)速度分布含(hán)有漩渦流分(fèn)量、軸向速度(dù)分布不對稱(chēng)性和扁平性(xing),使💔流量計計(ji)量産生誤差(chà),本文的算例(lì)中最大誤差(cha)達到了-1.79%。
(2)彎頭(tóu)與閥廣1開度(dù)之間的相對(duì)方向影響流(liú)量計的測量(liàng)精度📐,若流體(tǐ)通過彎頭和(hé)閥門時所産(chǎn)生的漩渦流(liu)方向相同♊，則(ze)增♊加了流量(liàng)計的計量誤(wù)差,反之💁則減(jiǎn)少計量誤☎️差(cha)。
(3)流量計中前(qian)導流件能有(you)效減少漩渦(wō)流強度,但在(zài)改💛善速度分(fèn)布的不對稱(cheng)性以及扁平(píng)性方面的效(xiao)🏃🏻‍♂️果并不明顯(xian)。

本文來源于(yú)網絡,如有侵(qīn)權聯系即删(shan)除！