摘(zhāi)要:平衡型(xing)低溫流量(liang)計
可用于(yu)低溫推進(jin)劑的加注(zhù)、分配、輸送(song)等環節,其(qí)孔闆結構(gou)特征是影(yǐng)響流量計(jì)性能的關(guan)鍵因素。爲(wei)了研究孔(kǒng)闆倒角對(dui)平衡型低(di)溫流量計(jì)流出系數(shu)、壓力損失(shi)系數和穩(wen)定性的影(ying)響,建立了(le)基于Mixture多相(xiang)流模型、Schnerr-Sauer空(kong)化模型和(he)Realizablek-ε湍流模型(xing)的CFD數值模(mo)型,并結合(hé)文獻中的(de)水翼空化(hua)實驗和多(duo)孔闆流動(dong)實驗的結(jie)果驗證了(le)模型的可(kě)靠性。模拟(nǐ)計算結果(guǒ)顯示,開設(shè)前倒角會(hui)增大多孔(kong)闆的流出(chū)系數,減小(xiǎo)壓力損失(shī)系數,但會(hui)增大流量(liàng)計測量時(shi)的不穩定(dìng)性;45°的前倒(dǎo)角使流出(chū)系數由0.674增(zēng)大到0.907,适當(dāng)開設前倒(dǎo)角可以有(you)效提高流(liu)量計的工(gong)作性能。而(er)開設後倒(dǎo)角對流量(liang)計性能的(de)影響較小(xiǎo)。用于流體(tǐ)流量的雙(shuāng)向測量時(shí),可對多孔(kong)闆的前後(hou)端均開設(shè)45°的倒角。
1引(yin)言
孔闆流(liú)量計
因其(qí)結構簡單(dān)、可靠性高(gao)和流體适(shi)用性廣等(děng)優點,目前(qian)已廣泛地(di)應用于石(shi)油和化工(gōng)等領域。然(ran)而,當流體(ti)流經孔闆(pan)時會發生(sheng)節流壓降(jiang),容易發生(sheng)空化現象(xiang),此外也會(huì)造成較大(dà)的局部壓(ya)力損失,這(zhè)會對流量(liàng)計的性能(néng)和設備安(ān)全帶來影(ying)響。另一方(fang)面,空間技(ji)術的快速(su)發展對低(di)溫流體流(liu)量測量精(jīng)度的要求(qiu)也越來越(yue)高[1]。低溫推(tui)進劑的加(jiā)注、分配、輸(shu)送等環節(jie)都離不開(kai)流量的精(jīng)度高測量(liang)。多孔闆可(kě)以平衡調(diào)整流場[2],流(liu)體流經多(duō)孔闆後受(shòu)到的擾動(dong)和壓力損(sun)失比标準(zhun)孔闆小,因(yin)而在低溫(wen)流體測量(liàng)領域的應(ying)用潛力大(da)。
在過去的(de)幾十年間(jian),多孔闆的(de)研究受到(dào)大量關注(zhu),主要集中(zhong)于結構參(cān)數和運行(hang)工況對其(qí)流出系數(shù)和壓力損(sǔn)失系數的(de)影。
可以發(fa)現,以前對(dui)多孔闆流(liú)量計的研(yán)究多集中(zhong)于常溫流(liú)體,如空氣(qi)和水等,對(dui)應用于航(hang)天推進技(ji)術領域的(de)低溫流體(tǐ)等研究相(xiang)對較少。此(ci)外,低溫流(liu)體流經多(duō)孔闆後易(yì)發生空化(huà)現象,在研(yan)究多孔闆(pan)流量計适(shì)用于低溫(wēn)流體的性(xing)能研究時(shi),需要建立(lì)并驗證考(kǎo)慮低溫流(liú)體空化流(liu)動的數值(zhi)模型。同時(shi),對孔闆結(jie)構參數的(de)研究多集(jí)中于孔闆(pan)直徑比、孔(kong)闆厚度、開(kai)孔直徑、孔(kǒng)分布方式(shì)等,很少涉(she)及到孔闆(pan)倒角。
拟以(yǐ)低溫流體(tǐ)液氮爲介(jie)質,采用數(shu)值方法研(yan)究孔闆倒(dao)角對平衡(heng)型流量計(jì)低溫流體(ti)流量測量(liàng)性能的影(yǐng)響,計算模(mo)型将考慮(lǜ)低溫流體(tǐ)的空化效(xiao)應。
2方法
2.1數(shù)學模型及(ji)驗證
液氮(dan)流經多孔(kong)闆後,因節(jiē)流壓降,在(zài)一定工況(kuàng)下流場壓(yā)力會小于(yu)相應溫度(du)下流體的(de)飽和壓力(li),誘發空化(huà),此時流體(tǐ)流動
爲氣(qì)液兩相流(liú)。将氣液兩(liǎng)相看成混(hun)合物單相(xiàng),采用混合(he)物多相流(liu)模型求解(jie)連續性方(fāng)程、動量方(fāng)程和能量(liàng)方程。基本(běn)控制
方程(cheng)如下
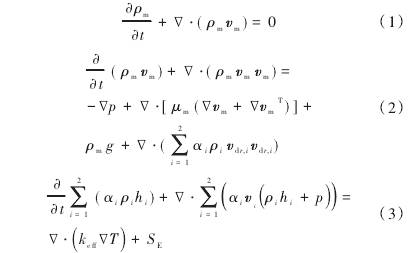
式中(zhong)下标m,l和g分(fèn)别表示混(hùn)合相、液相(xiang)和氣相;a爲(wèi)體積分數(shù);p,v,μ,t,p,T和h分别爲(wei)密度、速度(dù)、動力粘度(dù)、時間、壓力(li)、溫度和焓(hán);keff爲有效導(dao)熱系數;SE爲(wèi)體積熱源(yuan);?dr.;爲相i的漂(piao)移速度。
Schnerr-Sauer空(kōng)化模型已(yi)被用于低(dī)溫流體空(kōng)化的數值(zhí)計算[19-20]。其具(ju)體表達式(shi)爲[21]分别表(biao)示氣泡生(shēng)成、氣泡破(pò)裂和飽和(he)蒸汽。

此外(wài),采用Realizablek-ε湍流(liu)模型進行(háng)湍流閉合(hé),它滿足雷(léi)諾應力的(de)數學約束(shù),與實際湍(tuān)流過程一(yi)緻。與标準(zhǔn)k-ε模型相比(bǐ),改進了湍(tuān)流粘性的(de)計算,并基(ji)于均方渦(wō)波動的輸(shu)送方程建(jiàn)立了新的(de)ε方程。對涉(she)及旋轉、強(qiang)逆壓梯度(dù)下的邊界(jiè)層,分離和(hé)回流等流(liu)動,Realizablek-ε模型可(kě)得到較好(hǎo)的預測結(jie)果。湍動能(neng)k和湍流擴(kuo)散率ε的輸(shu)送方程爲(wei)
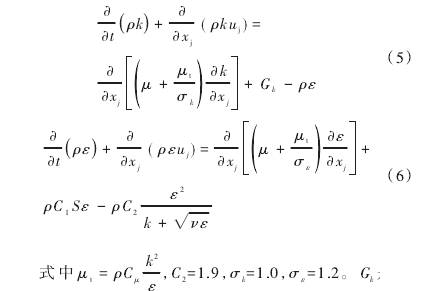
是因平均(jun)速度梯度(dù)生成的湍(tuan)動能。
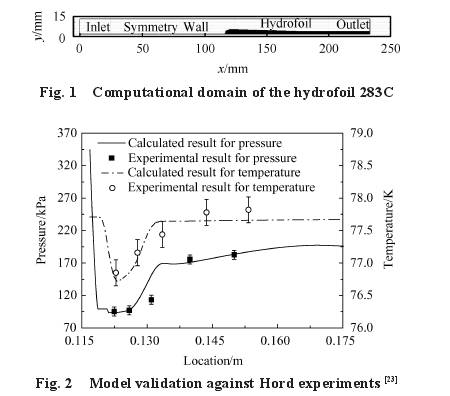
采用(yong)Hord等[23]的液氮(dan)水翼空化(hua)實驗283C來驗(yan)證上述數(shu)學模型在(zai)模拟低溫(wēn)流體空化(huà)流動時的(de)可靠性。水(shuǐ)翼結構和(he)計算域如(rú)圖1所示,且(qiě)實驗中液(yè)氮的進口(kǒu)溫度爲77.71K,自(zì)由來流速(sù)度爲14.5m/s,空化(huà)數爲1.8。模拟(nǐ)中采用速(su)度進口和(he)壓力出口(kǒu),y=0處設爲對(dui)稱邊界條(tiáo)件,壁面設(she)爲無滑移(yi)壁面。計算(suàn)結果和實(shi)驗結果的(de)對比如圖(tu)2所示。水翼(yi)壁面壓力(li)和溫度的(de)數值及随(suí)
位置的變(biàn)化規律基(ji)本吻合,考(kǎo)慮到實驗(yàn)誤差及模(mo)拟對實際(ji)問題的簡(jiǎn)化,可以認(rèn)爲數值計(jì)算模型可(kě)以有效地(di)用于模拟(ni)低溫流體(tǐ)
的空化流(liu)動。
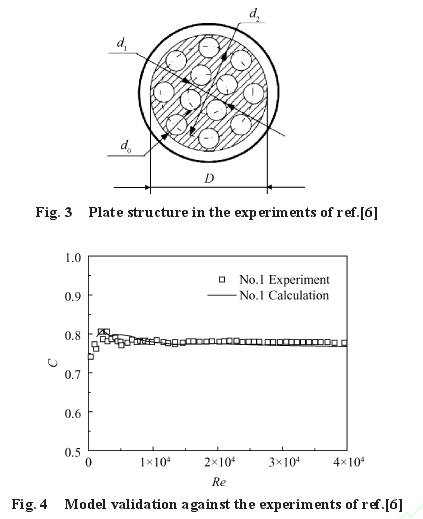
此外,選(xuan)取Huang等[26]的多(duō)孔闆流動(dòng)實驗結果(guo),來驗證數(shu)值模型用(yong)于流體多(duo)孔闆流動(dong)的準确性(xìng)。孔闆結構(gou)如圖3
所示(shì),采用了實(shí)驗中編号(hào)爲No.1的多孔(kǒng)闆,管路内(nèi)徑D、開孔直(zhí)徑d0、内圈開(kāi)孔圓心所(suo)在圓的直(zhi)徑d1和外圈(quan)開孔圓心(xīn)所在圓的(de)
直徑d2分别(bie)爲29mm,4mm,11mm和22.6mm,厚度(du)爲3mm;内圈開(kai)有5個孔,外(wài)圈開有9個(gè)孔。實驗工(gōng)質爲水,且(qiě)實驗在标(biao)準大氣
壓(yā)和室溫條(tiáo)件下開展(zhan)。模拟結果(guo)和實驗結(jie)果的對比(bǐ)如圖4所示(shi),兩者之間(jian)的相對誤(wù)差在4%範圍(wéi)内,從而驗(yàn)證了數值(zhi)模型用于(yu)多
孔闆流(liu)動模拟的(de)準确性。
2.2物(wù)理模型和(he)網格劃分(fen)
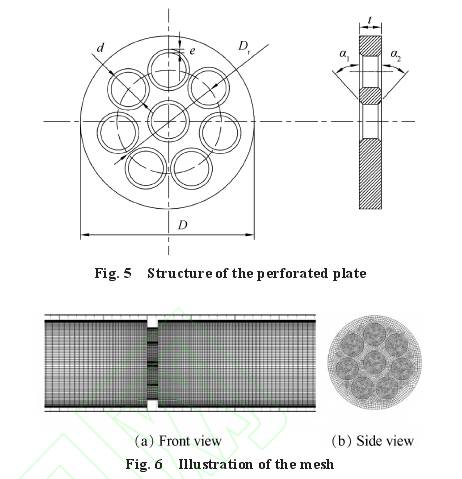
多孔闆結(jie)構如圖5所(suǒ)示。管路内(nei)徑D爲50mm,孔闆(pan)厚度t=6.35mm。多孔(kong)闆中心有(yǒu)一個孔;周(zhōu)圍孔分布(bu)于直徑Dr=30mm的(de)圓上,開孔(kong)數目爲7個(ge),其與中心(xīn)開孔直徑(jing)相同,均爲(wèi)d=10mm。控制倒角(jiao)圓與孔間(jiān)的距離差(cha)爲e=1mm。爲便于(yu)區分不同(tóng)倒角的多(duo)孔闆,以α1-α2表(biǎo)示前倒角(jiǎo)和後倒角(jiǎo)度數,分别(bié)爲α1和α2的多(duo)孔闆。多孔(kong)闆上下遊(you)直管段的(de)長度分别(bie)取10D和15D,以保(bao)證多孔闆(pan)上遊流動(dòng)充分發展(zhan),且下遊靜(jìng)壓力得到(dào)充分恢複(fu)。對計算域(yù)進行六面(miàn)體網格劃(hua)分,并對孔(kǒng)闆附近區(qu)域的網格(gé)進行局部(bu)加密,網格(gé)膨脹因子(zǐ)均小于1.2。劃(hua)分的網格(gé)如圖6所示(shì)。經過網格(ge)獨立性考(kao)核,計算中(zhōng)采用的網(wang)格總數約(yue)爲119萬。以不(bu)倒角時的(de)多孔闆爲(wèi)例,采用數(shù)量分别爲(wei)687310,1187590和1668615的三種(zhǒng)網格對液(yè)氮流經多(duo)孔闆時的(de)流出系數(shu)進行數值(zhi)計算,結果(guǒ)如圖7所示(shi)。與1668615的網格(ge)相比,采用(yòng)1187590的網格計(jì)算所得流(liú)出系數的(de)偏差小于(yu)0.3%。在保證計(ji)算精度的(de)同時,爲減(jiǎn)小運算量(liang),拟選用1187590的(de)網格劃分(fèn)方案。計算(suàn)域左端爲(wei)速度入口(kǒu),右端爲壓(yā)力出口,壁(bi)面爲無滑(hua)移邊界條(tiáo)件。
基于CFD軟(ruan)件ANSYSFLUENT14.5進行了(le)三維穩态(tài)數值模拟(nǐ)。壓力速度(du)耦合采用(yong)Coupled算法,并采(cǎi)用二階迎(yíng)風格式進(jìn)行數值求(qiu)解。空化發(fa)生時連續(xù)性方程和(he)氣相組分(fèn)的收斂标(biao)準設爲10-3,其(qí)餘設爲10-6。
3結(jie)果與讨論(lun)
計算中選(xuan)用液氮爲(wei)流體介質(zhì)(進口溫度(dù)爲77.36K,出口壓(ya)力爲0.2MPa),壁面(miàn)絕熱且無(wu)滑移。通過(guò)改變流體(tǐ)進口速度(du),可以得到(dao)不同雷諾(nuò)數下的流(liu)量計工作(zuo)性能。雷諾(nuò)數Re=uD/v,速度u取(qu)流體進口(kǒu)速度,特征(zheng)長度取管(guǎn)路内徑D,液(yè)氮的運動(dong)粘度爲0.001993cm2/s。采(cǎi)用流出系(xi)數和壓力(li)損失系數(shu)兩個無量(liàng)綱量來表(biao)征多孔闆(pǎn)流量計的(de)工作性能(néng)。流出系數(shu)爲
 實際流(liu)量與理想(xiang)流量的比(bi)值[24],其表達(da)式爲
實際流(liu)量與理想(xiang)流量的比(bi)值[24],其表達(da)式爲
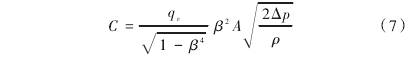
式中(zhong)qv爲流體體(tǐ)積流量,A爲(wei)管路橫截(jie)面積,Δp爲節(jie)流壓降;等(deng)效直徑比(bi)β=(Ah/A)1/2,Ah爲孔闆總(zong)開孔面積(ji)。壓力損失(shi)系數定義(yi)爲
![]()
式中△?是(shi)流體流經(jīng)孔闆的永(yong)久壓力損(sǔn)失,模拟中(zhong)取孔闆.上(shàng)遊1D和下遊(you)6D位置處的(de)壓力差。
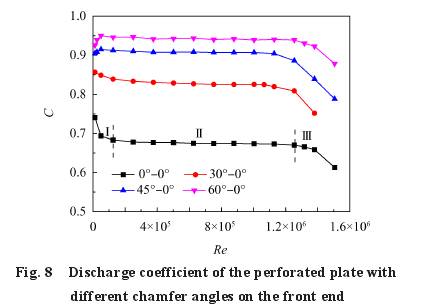
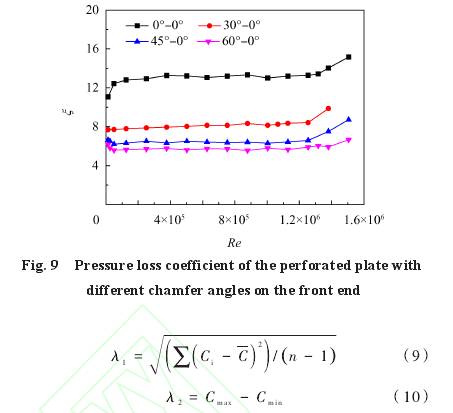
在(zài)多孔闆前(qián)端(與上遊(yóu)區域相連(lian)的部分)開(kai)孔處分别(bié)開設0°,30°,45°和60°的(de)倒角,後端(duān)不倒角,多(duō)孔闆流出(chū)系數C和壓(ya)力損失系(xì)數ξ随雷諾(nuo)數Re的變化(huà)分别如圖(tu)8和圖9所示(shì)。從圖中可(kě)以發現,随(suí)着Re的增加(jiā),孔闆流出(chū)系數和壓(ya)力損失系(xi)數的變化(hua)呈現出三(san)個階段,即(ji)不穩定區(qū)、穩定區和(he)空化區[10]。以(yi)無倒角時(shí)的工況爲(wei)例,三個階(jiē)段分别用(yong)I,II和III表示,如(rú)圖8所示。當(dāng)Re<1.2544×105,即進口速(sù)度u<0.5m/s時,流量(liàng)計處于不(bú)穩定區,流(liu)出系數随(suí)Re的增大而(er)減小,此時(shí)影響流出(chu)系數的流(liu)束收縮系(xi)數和孔闆(pan)總阻力系(xì)數會随Re發(fa)生變化。當(dang)Re>1.2544×106,即進口速(sù)度u>5m/s時,流量(liang)計處于空(kōng)化區,流體(ti)流經多孔(kǒng)闆後因節(jiē)流壓降而(er)發生空化(huà),氣液兩相(xiàng)流動的存(cún)在使流量(liang)計壓降增(zeng)大,造成流(liú)出系數的(de)下降,影響(xiǎng)流量計的(de)工作性能(néng)。此外,還會(huì)帶來侵蝕(shi)、振動和噪(zào)聲等危害(hai)。當1.2544×105<Re<1.2544×106時,流束(shù)收縮系數(shù)和孔闆總(zong)阻力系數(shù)不再随Re變(biàn)化,因而流(liu)出系數基(jī)本不随Re發(fa)生變化,此(cǐ)時流量計(ji)處于穩定(ding)區。
流量計(ji)在正常工(gōng)作時,須處(chu)于中間的(de)穩定區域(yù),此時多孔(kǒng)闆的流出(chu)系數和壓(yā)力損失系(xì)數基本不(bu)随Re發生變(bian)化。流出系(xi)數越大,壓(yā)力損失系(xì)數越小,且(qie)穩定工作(zuò)區域流出(chu)系數的波(bo)動越小,意(yì)味着流量(liàng)計的性能(neng)更優、更穩(wěn)定。與無倒(dǎo)角(0°-0°)的工況(kuàng)相比,多孔(kong)闆開設前(qian)倒角後,流(liú)出系數明(ming)顯增大,且(qiě)随前倒角(jiao)度數的增(zeng)大而升高(gāo)。當倒角分(fen)别爲0°,30°,45°和60°時(shi),穩定區域(yu)的平均流(liu)出系數分(fen)别爲0.674,0.828,0.907和0.942。類(lei)似地,多孔(kong)闆壓力損(sǔn)失系數随(suí)前倒角度(dù)數的增大(dà)而下降。
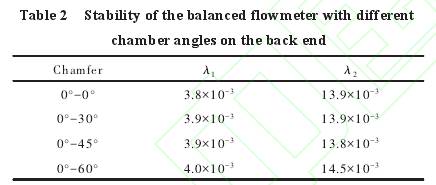
采(cǎi)用标準差(chà)λ1和線性度(dù)λ2來評估多(duo)孔闆流量(liang)計工作區(qū)間(即穩定(ding)區)的穩定(ding)性
指标數(shù)值越小,表(biǎo)示流出系(xì)數波動越(yuè)小,流量計(jì)的穩定性(xìng)越高。表1列(liè)出了不同(tóng)前倒角時(shi)流量計工(gong)作區間的(de)穩定性指(zhi)标。由表中(zhong)數據可以(yǐ)看到,前倒(dao)角的引入(rù)會在一定(dìng)程度上降(jiàng)低流量計(jì)的穩定性(xìng)。
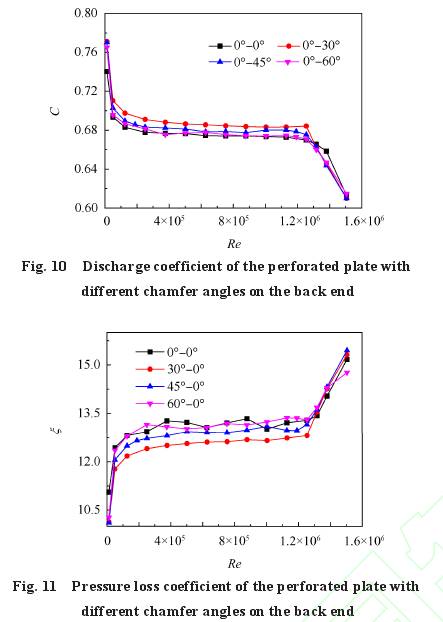
多孔闆前(qian)端不進行(háng)倒角,後端(duān)則分别有(you)0°,30°,45°和60°的倒角(jiǎo)時,流出系(xi)數和壓力(li)損失系數(shù)随Re的變化(hua)分别如圖(tú)10和圖11所示(shi)。開設後倒(dao)角對多孔(kong)闆流出系(xi)數和壓力(li)損失系數(shù)的影響較(jiao)小,後倒角(jiao)爲60°時,穩定(ding)區間的平(píng)均流出系(xì)數和壓力(lì)損失系數(shu)分别爲0.676和(he)13.159,這與沒有(you)倒角時的(de)數值0.674和13.173非(fei)常接近。計(ji)算結果表(biao)明,開設後(hòu)倒角會增(zēng)大流出系(xì)數,降低壓(yā)力損失系(xì)數,且随着(zhe)倒角度數(shu)的增大影(ying)響将變小(xiao)。當後倒角(jiǎo)爲30°時,工作(zuo)區間的平(ping)均流出系(xì)數從0.674變爲(wei)0.686,提高了1.78%;平(píng)均壓力損(sun)失系數由(you)13.173變爲12.623,降低(dī)了3.90%。流量計(ji)工作區間(jiān)流出系數(shu)的穩定性(xìng)指标如表(biao)2所列。與前(qián)倒角相比(bǐ),後倒角對(dui)流出系數(shù)穩定性的(de)影響較小(xiǎo)。

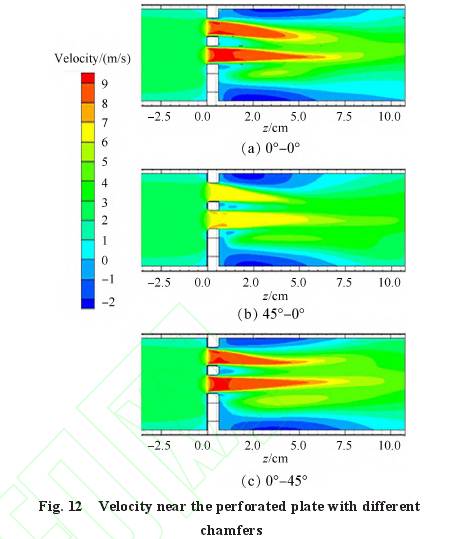
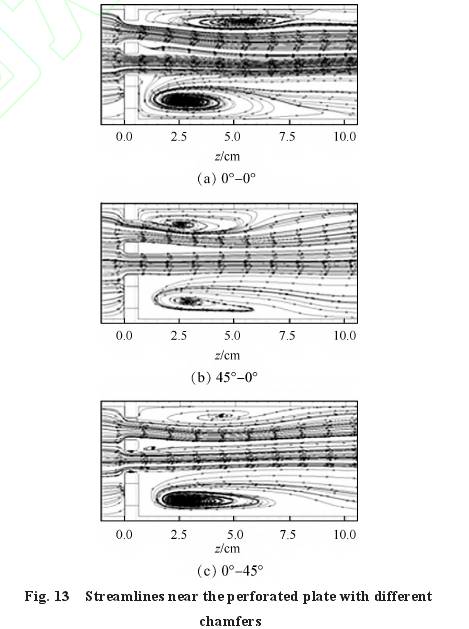
倒角對多(duō)孔闆工作(zuò)性能的影(ying)響是通過(guò)改變節流(liú)孔附近的(de)流場引起(qi)的。流體流(liú)經多孔闆(pǎn)後的永久(jiu)壓力損失(shi)包括進口(kou)處的流動(dong)阻力(即多(duo)孔闆本身(shēn)造成的局(ju)部壓力損(sun)失)、多孔闆(pǎn)下遊區域(yù)流場中旋(xuan)渦運動消(xiāo)耗的能量(liang)和管道内(nèi)壁面處的(de)沿程損失(shi)[13]。沿程損失(shi)不受倒角(jiǎo)的影響,下(xià)面的分析(xī)中将不作(zuò)考慮。0°-0°,45°-0°和0°-45°三(sān)種倒角方(fang)式下多孔(kǒng)闆附近的(de)速度雲圖(tú)和流線圖(tu)如圖12和圖(tú)13所示。液氮(dan)進口流速(sù)爲2m/s。
沒有倒(dǎo)角時,流體(ti)從上遊管(guan)路進入截(jié)面突然收(shou)縮的節流(liú)孔,進口處(chù)流動阻力(li)大;流束在(zài)節流孔處(chù)收縮,流線(xiàn)距壁面較(jiào)遠,流體流(liu)經節流孔(kǒng)後形成的(de)射流速度(du)較高,下遊(you)壁面存在(zài)較長的回(hui)流區域,流(liu)體旋渦運(yun)動消耗的(de)能量較多(duō)。開設前倒(dǎo)角後,流體(tǐ)沿着倒角(jiǎo)進入節流(liú)孔,緩解了(le)流體在進(jìn)入節流孔(kong)時截面突(tu)然收縮的(de)過程,使流(liú)體沿進口(kou)邊緣轉向(xiang)時的流動(dòng)比較平穩(wěn),流線更加(jia)貼近壁面(mian),孔闆截面(miàn)與流線的(de)變化較爲(wèi)一緻,從而(er)減小了進(jin)口處的流(liú)動阻力;此(ci)外,與無倒(dao)角時相比(bi),開設前倒(dao)角後射流(liú)的速度以(yi)及孔闆下(xia)遊回流區(qu)的長度也(ye)明顯縮短(duǎn),流體的流(liú)動損失減(jiǎn)小。而開設(shè)後倒角對(dui)流束收縮(suō)和流速大(dà)小的影響(xiang)相對較小(xiao),下遊壁面(mian)附近回流(liu)區的長度(du)略有縮短(duan),流體流經(jīng)孔闆後的(de)壓力損失(shī)略有下降(jiàng)。
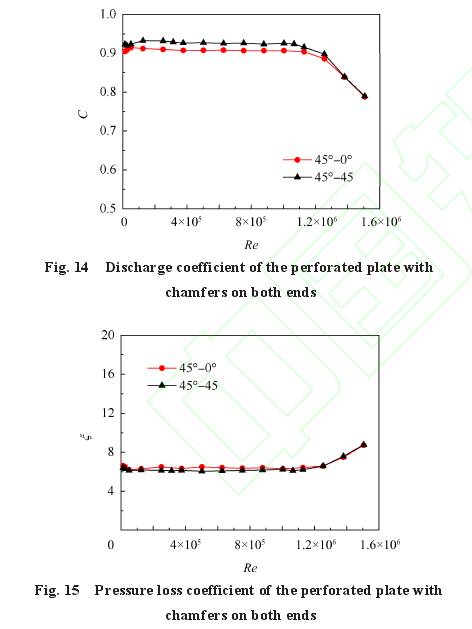
爲便于流(liu)體流量的(de)雙向測量(liàng),對多孔闆(pǎn)前後倒角(jiǎo)均爲45°的工(gong)況也進行(háng)了研究,流(liu)出系數和(hé)壓力損失(shī)系數的變(bian)化如圖14和(hé)圖15所示。相(xiàng)比于隻開(kāi)設前倒角(jiǎo)的工況,前(qian)後均進行(háng)倒角時多(duo)孔闆的流(liú)出系數略(luè)有增大,壓(yā)力損失系(xì)數略有下(xià)降。具體地(di),流量計工(gong)作區間的(de)平均流出(chu)系數由0.907增(zēng)大到0.927,平均(jun1)壓力損失(shī)系數由6.403減(jiǎn)小到6.135。
4結論(lùn)
采用數值(zhí)方法,研究(jiu)了多孔闆(pǎn)倒角對平(ping)衡型流量(liàng)計工作性(xìng)能的影響(xiǎng),主要結論(lùn)有:
(1)孔闆開(kāi)設前倒角(jiao)後,流出系(xì)數增大,壓(yā)力損失系(xì)數減小,但(dan)前倒角的(de)引入會在(zài)一定程度(dù)上增加流(liú)量計流量(liang)測量時的(de)不穩定性(xìng)。前倒角分(fen)别爲0°,30°,45°和60°時(shí),穩定區域(yu)的平均流(liu)出系數分(fen)别爲0.674,0.828,0.907和0.942。與(yǔ)開設前倒(dao)角相比,開(kāi)設後倒角(jiao)對流量計(jì)工作性能(néng)的影響較(jiao)小。相比于(yú)隻開設前(qián)倒角的計(jì)算工況,前(qian)後均倒角(jiǎo)時流量計(ji)平均流出(chu)系數略有(yǒu)增大,壓力(lì)損失系數(shù)略有下降(jiang)。
(2)倒角對多(duo)孔闆工作(zuo)性能的影(yǐng)響是通過(guò)改變節流(liu)孔附近的(de)速度分布(bù)和流線引(yin)起的。
以上内(nei)容源于網(wǎng)絡,如有侵(qin)權聯系即(jí)删除!